Energy as we know it is mysterious, and it is the driving force behind all physical events in the universe. Robert Mayer, a German medical doctor who proposed the concept of energy, believed that energy is not matter, but it is real and can exist independent of matter. To this day, scientists do not know exactly what energy is. This lack of knowing prompted Richard Feynman, a Nobel prize physicist, to say that energy is an “abstract thing” and that physicists have no knowledge of what exactly it is.
Although energy is mysterious, scientists have uncovered two fundamental laws that govern its behavior. The first of these laws states that energy is “conserved”, which is the same thing as saying the “energy of the universe is constant”. While the second law states that energy flows by itself from a hotter substance to a colder substance, which is also the same thing as saying the “ENTROPY” of the universe increases.
So, what do we mean when we say that energy is conserved?
When we say energy is conserved, we usually mean that energy cannot be created nor destroyed, but it can be converted from one form to another. And as we convert energy from one form to another, energy in itself remains unchanged before and after the conversion. How did scientists come to the conclusion that energy cannot be created? Longtime ago engineers tried several times without success to make a “perpetual motion machine” —– a machine that can run without using external fuel, heat, or power.
How did scientists come to the conclusion that energy is conserved?
Imagine that energy spreads out as heat from your hot cup of coffee into the cooler surrounding air. From the first law, we can be sure that the total energy in your cup of coffee is unchanged— it simply spreads into the cooler surrounding air molecules as heat. As a result, we can say that the energy lost by the coffee is equal to the energy absorbed by the surroundings. Another example is that, imagine that an apple of mass, m and velocity, v hangs above the ground at a height, h on a tree. When this apple is cut loose and travels vertically toward the ground, we can calculate its kinetic energy (K.E.) by using the formula: K.E. = ½ mv2. And we can also calculate its potential energy by using the formula: P.E. = mgh, where g is the acceleration due to gravity. When we add the value of its kinetic energy to the value of its potential energy, we will get its total mechanical energy (E). That is:
E = ½ mv2 + mgh
As the apple moves toward the ground, its potential energy decreases, while its velocity and kinetic energy increases so as to keep its total mechanical energy (E) constant. As a result, the sum of its potential and kinetic energy remains constant, even though one of the two must increase at the expense of the other. This behavior of the apple as it falls from a height illustrates the fact that energy is conserved. If energy is conserved, then it follows that an increase in energy in one system must be compensated by a loss of an equal amount of energy from another system. As a result, we can’t create or destroy energy, but we can transfer it from one system to another.
So how can we transfer energy from one system to the other?
We can transfer energy by WORK AND by HEAT. So, what is work? Work is defined as force times the distance through which it acts. Mathematically, we can express work as: work = force x distance. Work is usually the means by which energy is transferred mechanically between a system and its surroundings, just like the falling apple discussed earlier. And what is heat? Heat, like work, is not a material substance. Heat is a way by which energy is transferred between a system and its surroundings as a result of a difference in temperature. Now, let’s further explain this by considering the following: imagine that we added a certain amount of energy as heat, q to a system. Since energy must be conserved, it follows that the energy added as heat must appear as work (w) done by the system or appear as a change in the internal energy (ΔE) of the system. Mathematically, we can express this law of conservation of energy and sometimes called the first law of thermodynamics as:
q = ΔE + w —–(1), which we can rearrange to get:
ΔE = q – w ———-(2)
Clearly, the first law of thermodynamics places restrictions on what processes are allowed in nature. For instance, if you want to build a rocket to carry you to mars, you must first figure out how much fuel you will need to burn to power your rocket from here to there.
Although the first law tells us that energy is conserved, we can’t apply it to explain why when energy changes forms most of it spreads out as heat, and once it spreads out as heat it is difficult to recycle it into useful forms of energy even though it is present to satisfy the first law.
To understand why energy spreads out as heat, we have to turn to the second law of thermodynamics. If you recall, it states that energy flows naturally from a hotter substance to colder substance. To illustrate this, let’s imagine that on your way home you bought a cup of hot coffee and can of cold sprite and placed both in the same bag. Upon arrival at home, you noticed that the can of sprite had become warmer, while the cup of coffee had become cooler. Then, you asked yourself why not the other way around? After staring wildly at your drinks, you realized that it is the way it is — energy always flows downhill from hot to cold and not uphill from cold to hot. As a result, you can’t recycle the heat absorbed by the sprite and put it back in the coffee. Similarly, you can’t recycle the heat generated by your car to run it in order to reduce your gas cost at the pump, which is why we must use our energy resources wisely.
So how can the second law be expressed mathematically?
As you can see, when energy is transferred, some of it is used to do work, while some spreads out as heat. In search of why it spreads out as heat, Clausius, a German scientist, figured out that when energy is transferred downhill, for instance, from a cup of coffee to the surrounding air, the ratio of the amount of heat flow to temperature in Kelvin always increases regardless of the things involved. Clausius named this ratio ENTROPY, which means transformation in Greek. Mathematically, we can express Entropy as:
ΔS = ΔQ/T
where ΔS is the entropy change, ΔQ is the amount of heat flow, and T is temperature in Kelvin. Although Clausius clearly generated an expression for entropy, he could not explain what it meant? In an attempt to figure out what entropy meant; another scientist called James Maxwell had to turn to the behavior of gas molecules at the molecular level. But understanding the behavior of these minute particles at the molecular level was a huge task for Maxwell. It was a challenge because at the molecular level molecules are many and are invisible to our eyes. Because of this, Maxwell could not describe the motion of these particles with 100% certainty. As a result, he turned to probability to help him study the behavior of these particles. But first, to do this, Maxwell had to turn to the “Billiard Ball Model.” This model was popular and widely accepted model used to describe gas behavior in the eighteenth century. This model was based on the assumption that gases consist of tiny invisible particles with no attractive forces between them but were constantly moving and colliding with the walls of their container to generate pressure. Although this was true, no one back then had determined the speed of these particles. As a result, Maxwell set out to do just that by using calculus probability to do his calculations. When Maxwell plotted the results of his calculations on a graph, it appeared like so:
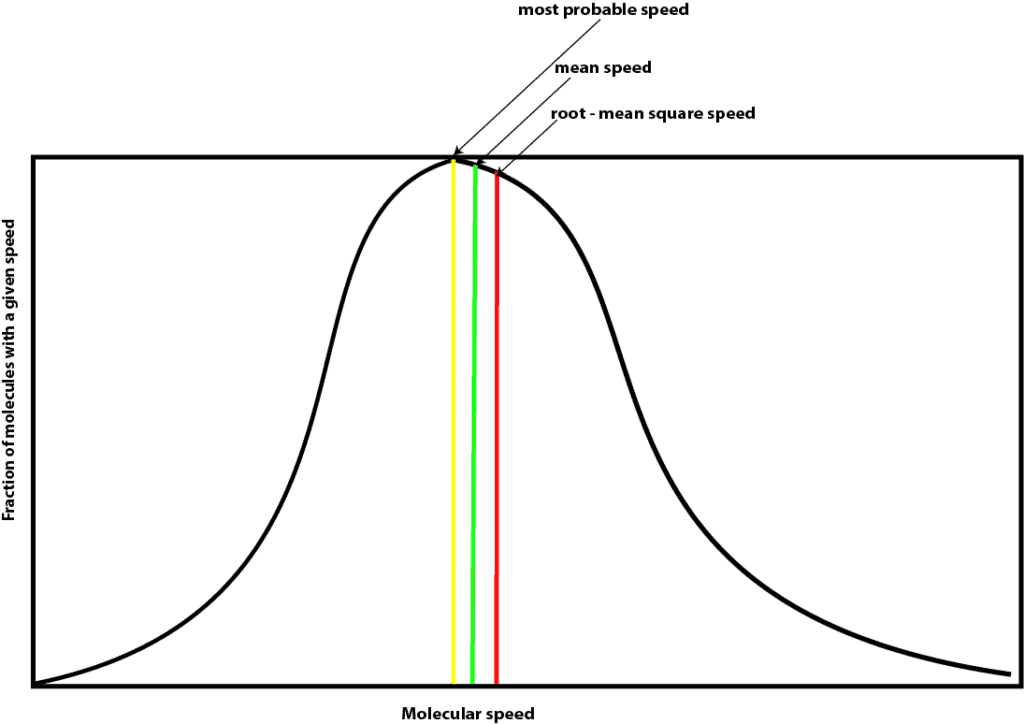
As you can see, Maxwell plotted the fraction of molecules with a given speed on the y-axis and their speeds at a particular temperature on the x-axis. As you can tell, this curve resembles the widely known bell curve that is sometimes used to curve our grades at school. As you are well aware, most often the distribution of our class grades after taking an exam sometimes fits a bell curve perfectly. And when it does, you usually notice the following:
- few people perform exceptionally high
- few people perform exceptionally low
- most people perform between these two extremes
Similarly, what the graph above is telling us about gas behavior at a particular temperature is that:
- few molecules have low speed
- few molecules have high speed
- some molecules have higher speed, but this speed peaks at a certain point and then stars to drop
- Many molecules have speed that correspond to the peak of the curve. This speed is called the most probable speed, which is shown in yellow on the graph
As you can see, Maxwell’s gas theory was impressive, as a result, it was immediately accepted by many of his peers. However, Maxwell fell short to apply it to explain ENTROPY. But he opened the door for an Austrian scientist called Ludwig Boltzmann to modify it to explain ENTROPY. Boltzmann recalled that Maxwell developed his gas theory based on the billiard ball model. And the billiard ball model was developed based on the simple assumption that gas molecules are too far apart to interact with each other. As a result, the only energy gas molecules had was kinetic energy. Although true, but the assumption omitted one important thing Boltzmann knew. In the real world, Boltzmann knew that when conditions are right, molecules can attract each other to form bonds and these bonds can store potential energy just as compressed springs do. As a result, Boltzmann decided to work on Maxwell’s theory to account for these kinds of energy so that he could generalize it. Today, the graph Boltzmann derived for the speeds of gas molecules is widely called “Maxwell-Boltzmann distribution, which is similar to the graph above.” Armed with this new knowledge of gas behavior, Boltzmann had unlocked the door on how to apply molecular behavior to explain ENTROPY. But first, Boltzmann had to reason that entropy as a ratio of heat to temperature is a macroscopic quantity that can be determined in the laboratory with basic instruments like scales, thermometers, and pressure gauges. As a result, just like mass and energy, it is additive and does not reflect how these gases rearrange at the molecular level. He then imagined that if you join two identical flask containing gases at the same temperature such that the gases can flow into each other, then, you can say that the gas molecules will have twice the volume, twice the energy, twice the mass, and twice the entropy of what they initially had before you joined them. But an interesting question came up: what are the possible ways these molecules can rearrange as their collective macroscopic properties double? To answer that, just like Maxwell, Boltzmann fell back on probability — a game of chance— to help him out. To simplify things, just imagine that each flask contained 3 gas molecules with varying speeds: 1 slower-; 1 higher-, and 1 an average speed that reflects the temperature of the flask. Without changing any conditions, we can say that there are 3 possible ways we can assign a speed to a molecule in each flask. Now, when we join the two flasks, the number of ways one molecule from one flask and another molecule from the other flask can distribute themselves as a pair is not 6 but 15. This is because each of the molecules in one flask can pair up with each of the molecules from the other flask. From this calculation, you will notice that at the molecular level there are multiple ways in which these molecules can pair up and still maintain their macroscopic properties. But entropy, as Boltzmann saw it, is additive and a macroscopic level property. So, Boltzmann asked himself, how can he relate probability, which is multiplicative to entropy, which is additive? Boltzmann had an answer. He predicted that entropy was related to the logarithm of probability. Mathematically, this relationship is expressed as:
ΔS = KbInΩ,
where Kb is Boltzmann constant that relates kinetic energy to temperature, while Ω represents the number of microstates or ways in which molecules in a system can rearrange without changing the macroscopic properties of the system. As such, when the number of ways is high, the arrangement is common, and when it is low, the arrangement is rare. For example, when you toss 8 coins, an outcome of 4 heads is common than an outcome of 8 heads. This is because there are many ways of getting 4 heads but only one way of getting all heads. Now, let’s relate this to gas molecules trapped in a vessel as shown below:
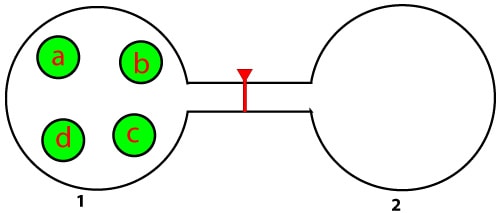
As you can see, the tube that connects vessel 1 to vessel 2 is sealed off to prevent air molecules from moving from vessel 1 to vessel 2. Vessel 1 holds four gas molecules labelled a, b, c, and d, while vessel 2 is empty (vacuum). Now, when the seal is broken, the molecules in vessel 1 will move fast and at random from vessel 1 to vessel 2 until equilibrium is established. And once equilibrium is established, the pressure in vessel 1 will be equal to the pressure in vessel 2. Now, as time passes the four molecules in both vessels can rearrange in many ways to maintain the equilibrium. So, the question is: in how many ways can the four molecules rearrange such that there are two molecules in vessel 1 and two in vessel 2? Now, with some thinking and sketching, I came up with these diagrams:
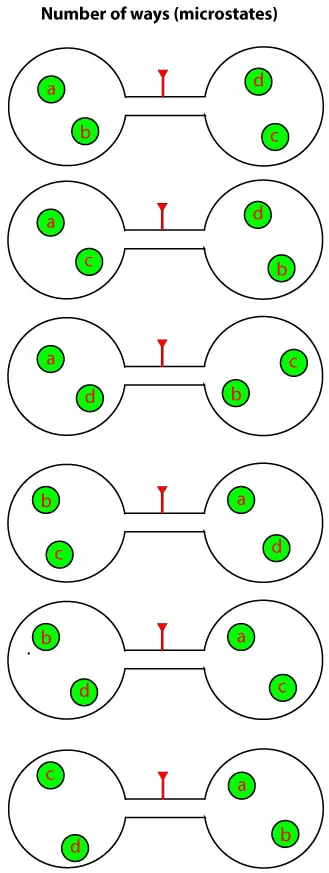
As you can see, there are six possible ways in which the molecules can rearrange such that there are two of them in each vessel. Now imagine that we have 50 molecules to determine this arrangement. As you well know, this would be tedious. But fortunately, we have an easy way out. And this easy way out usually involves BINOMIALS. That is the number of microstates in a given state can be calculated using the binomial coefficient:

Now, as you can see it is easy to determine the number of microstates using the binomial expression. But let’s say we wanted to determine the total number of ways the four molecules can possibly rearrange in the two vessels; how do we go about this? Easy. We just have to remember that the total number of microstates (W) is given by the expression
W = 2n
where the superscript, n is the number of molecules. Therefore, the total number of ways the four molecules in our example can possibly rearrange is: W = 24= 16.
Now, imagine that we want to determine the probability of having two molecules in the left vessel and two in the right vessel. How do we go about this? To determine the probability, you must divide the number of microstates by the total number of microstates. Therefore, in our example, we determined that there were 6 ways (microstates) of having two molecules in each vessel. And we also determined that there was a total of 16 microstates. As a result, the probability of having two molecules in each vessel is 6/16 = 3/8 = 0.375.
Now let’s stretch our example a little bit. What’s the probability of having the four molecules rearrange such that there are four molecules in each vessel? To do this, I will do the following:
Step 1
Calculate the number of microstates
Thus, microstates = 4!/4!(4-4)! = 4!/4!0! = 4x3x2x1/4x3x2x1x1 = 1
Step 2
Calculate the total number of microstates = 24= 16
Step 3
Calculate probability = 1/16 = 0.0625
So, what is ENTROPY?
As you can see, there is only one way the molecules can rearrange such that you have all four molecules in one vessel. While there are six ways in which the four molecules can rearrange such that you have 2 molecules in each vessel. So, what does this tell us about ENTROPY. It tells us that ENTROPY measures the degree of randomness, and randomness implies disorder. Therefore, ENTROPY is disorder, and nature prefers disorder over order. Nature prefers disorder because disorder is more likely to occur than order, which is why the energy from your hot cup of coffee spreads into the surroundings as heat, but difficult to gather and put back in your coffee. Similarly, anytime you drive your car, the entropy of the universe increases. This is because the energy packed in the gas you buy to run your car ends up in the surroundings as heat. So, watch out for heat!
