What’s the ideal gas equation and what does it measure?
The ideal gas equation relates pressure, volume, moles, and temperature of gas. We use it as a model to predict and explain gas behavior under a particular set of conditions. The ideal gas equation is mathematically expressed as:
- PV = nRT
Where
- P is pressure
- V is volume
- n is amount of gas measured in moles
- R is universal gas constant
- T is temperature measured in Kelvin
How can you derive the ideal gas equation?
You can derive the ideal gas equation when you relate pressure, temperature, amount and volume to one another as you study the behavior of gas under a particular set of conditions. When you do, you will find that:
- P ∞ 1/V, when you hold temperature (T) and amount (n)constant
- V ∞ T, when you hold pressure (P) and amount (n) constant
- P ∞ n, when you hold temperature (T) and volume (V) constant
- V ∞ n, when you hold pressure (P) and amount (n) constant
- P ∞ T, when you hold amount (n) and volume (V) constant
From these relationships, you can see that pressure is inversely proportional to volume (1), but directly proportional to temperature (5) and amount (3). You can also see that volume is directly proportional to temperature (2) and amount (n). Since these variables relate to one another in a precise way, you can remove the proportionality sign and introduce an equal sign and a proportionality constant, R. If you do, you will get:
When you look on the left side of equations 1 to 5, you will notice that only pressure and volume appear. And on the right side of equations 1 to 5, only temperature and amount appear. You will also notice that pressure and volume are each directly proportional to temperature (2,5) and amount (3,4). Since pressure is inversely proportional to volume, but directly proportional to amount and temperature, you can write that
- P∞nT/V (which is the same as V∞nT/P)
If you remove the proportionality sign and introduce a proportionality constant, R, you will get
- P = RnT/V
If you multiply both sides of the equation by V, you will get the ideal gas equation
- PV = RnT
Where R is gas constant, whose value you can determine by experiment.
How can you determine the units of R?
To determine the units of R, you must first decide on the units in which to measure the other variables in the ideal gas equation. If you measure
- pressure (P) in atmospheres (atm),
- Volume (V) in liters (L)
- Amount of gas (n) in moles (mol)
- Temperature (T) in kelvins(K),
then we can determine the units of R as:
- PV = nRT
- atm x L = mol x R x K
If we isolate R by dividing both sides of the equation by mol and K, we will get
- atm x L/mol K = mol x R x K/mol K
Thus, R = atm L/mol K
How can you determine the value of R?
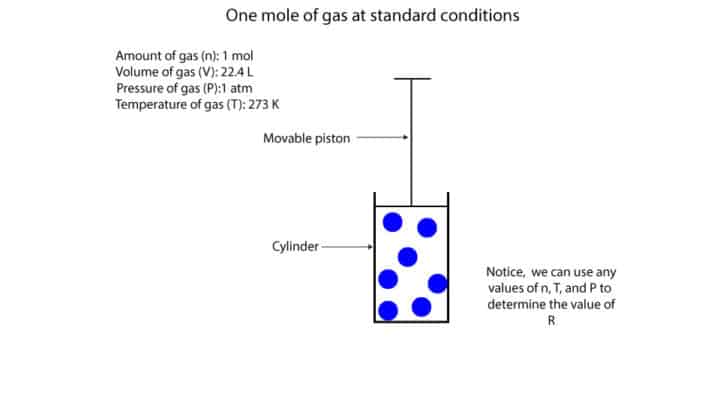
You can determine the value of R when you use the piston-cylinder model to hold a sample of 1 mole of gas at standard conditions. Standard conditions as used here means 1 mole of gas at a pressure of 1 atm and at a temperature of 273 K (0 °C).
How can you determine the volume of 1 mole of gas in our model?
Easy! You let the movable piston come to a complete stop on its own and then you measure the gas volume. Once you do, you will notice that the volume of 1 mole of gas is 22.4 L. Here is a model to show the cylinder-piston set up.

Now, when you substitute the values for P, T, n, and V into the ideal gas equation, you can solve for R like so:
- PV = nRT
- (atm) (22.4 L) = (1.00 mol) (R)(273K)
When we isolate R, we will get
- R = (1.00 atm) (22.4 L)/ (1.00 mol) (273 K)
- R = 0.0821 atm L/mol K, called the universal gas constant
Notice, when solving ideal gas law problems, you must ensure that the units of pressure, temperature, and volume are consistent with the units of the universal gas constant (R).
If the units aren’t consistent with R, you must convert them. Recall that;
- 1 atm = 760 mm Hg and 1 atm = 760 torr
- 0 °C + 273 = K
- 1000 mL = 1 L
From these relationships, you can create conversion factors to convert from one unit of measure to another.
To learn how to convert from one unit to another, click here.
To learn about the general properties of gases, click here.