When you measure something, the significant digits include all the certain and uncertain digits in the measurement. Together, these digits usually reveal reliable information, but with the last digit being the uncertain one in the measurement. Thus, the greater the number of significant figures the more certain the measurement. Now, let’s use the following illustration to clarify our point:
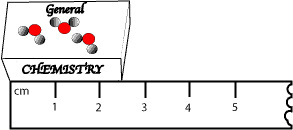
For instance, let’s assume that we have a really small general chemistry textbook, and we want to determine the length of this textbook. So, our friend Peter placed a ruler along its spine and read a value of 2.4 cm as its length. And you also followed Peter and read a value of 2.5 cm as its length. From these values, we can say that the number of significant digits in both measurements is two. However, the uncertainty (guessing) associated with these measurements lies in the last digit of the measurement. That is the 2.4 cm and 2.5 cm is uncertain in the tenths place. To resolve this, Mary, our best friend decided to take the final reading, and so she read a value of 2.5 cm, which agrees with yours.
To keep Peter happy, Mary decided to calculate the amount of uncertainty. To do this, she looked at the graduations on the ruler and noticed that it has 1 cm divisions. Since the 1 cm division is too large, Mary imagined 10 subdivisions within the 1 cm. Which means if we divide 1 cm by 10, we can estimate the length of the book to 0.1 cm (one-tenth of a division). Therefore, we can write that the uncertainty of using the ruler is ±0.1 cm (read as plus or minus 0.1 cm). Which means the length of the textbook can be reported as 2.5±0.1 cm. Meaning the length of the textbook can be any number from 2.4 cm (2.5 cm – 0.1 cm) to 2.6 cm (2.5cm + 0.1 cm).
To keep track of this uncertainty, we usually follow some simple rules when adding, subtracting, multiplying and dividing measured values when solving numerical chemistry problems. To learn about these rules, click here and if you would like to learn about errors in measurement click here