What’s Density?
Density is the amount of matter (mass) packed in a given amount of space called volume. Mathematically, density (D) is expressed as a ratio of mass (m) to volume (v). Thus, D = m/v.
Density is an intensive physical property. This means that density does not depend on the amount of substance present. However, the variables mass and volume which are used to determine density are extensive properties. Extensive property is a property that depends on the amount of substance present. Let’s use the following models to explain this further:
As you look at the models above, you will notice that all three objects occupy the same amount of space (see sizes of squares). However, there are more atoms of iron packed in that same amount of space than there are molecules of glass and wood. If an atom of iron has more mass than a molecule of glass or wood, then clearly, iron will be more dense than glass or wood. This is so because if we divide each object’s mass by its volume, and since all three objects have the same volume, the object with the larger mass will have the greatest density. And the object with the smaller mass, will have the lowest density. Therefore, since particles differ in how they pack in three dimensional space, we can use density to identify a substance, which is why it is an intensive property.
Can density be determined graphically?
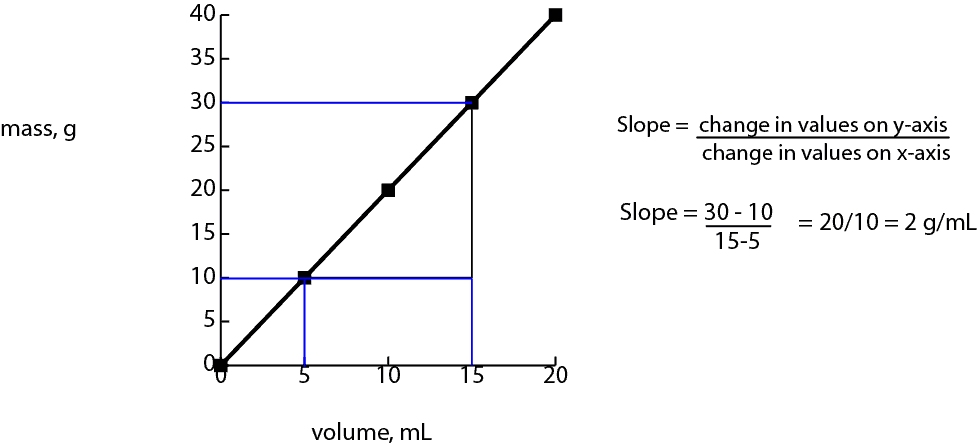
Yes, it can. Graphically, when you plot varying mass of substance on the vertical axis (y-axis) against its corresponding volume on the horizontal axis (x-axis), you will notice a straight line running through the data points, and as the mass of substance increase, the corresponding volume increase as well. Thus, the volume of substance increase in proportion to its mass. Now, let’s use the graph below to illustrate the concept.
Since its a straight line, you can easily calculate the slope of the line by choosing two data points on the line and tracing (tracing is shown in blue) their corresponding values on the y-axis (mass) and on the x-axis (volume). Next, you find the difference between the values on the y-axis and the difference between the values on the x-axis.
Finally, you divide the difference from the y-values by the difference from the x-values. Thus, from the graph above, slope = 2 g/mL. This slope we just determined has a special name called Density.
What math formula can we use to describe density?
Mathematically, density can be expressed as: Density = mass/volume (mass divided by volume) or D = M/V.
Mass is usually measured in grams or kilograms, while volume is measured in milliliters, liters or cubic centimeters.
Keep in mind that volume has two meanings in measurement;
- first, amount of space an object takes up
- second, amount of somethings an object can hold
In the density formula, V stands for the amount of space something takes up.
Since molecules differ in how they pack in a substance, chemists can use density to identify a substance.
What do we need to calculate the density of a substance?
We need to measure the mass and volume of our substance. To measure mass, you put your substance on a balance or a scale and record its mass in grams. To measure the volume of a liquid, you will need to pour the liquid into a graduated cylinder.
How do we measure the volume of an irregular object?
We need to use the water-displacement method. So what is the water-displacement method? It simply means the amount of water a sinking object pushes out of the way when it is placed in water.The amount of water that gets pushed away (displaced) is always equivalent to the objects volume. Let’s use these models to illustrate the concept.
The water level in cylinder A rises to a new level after you put a rock in it. So the volume of your object is the amount of water displaced. You can find this volume by subtracting the initial volume of water from the final volume of water in the cylinder. Notice that you can use the same approach to determine the volume of a regular object that sinks but does not dissolve in water.
In addition to the water-displacement approach, you can also use mathematical formulas to determine the volume of an object. For example, to determine the volume of a rectangular prism, you can multiply its length by its width by its height.
Can two objects have the same mass but different densities?
Yes! Keep in mind that density is a ratio of mass to volume. So if two objects have the same mass but different volumes, you should expect their densities to be different. Here is a model to illustrate the concept.
To depict equal masses, I have conserved the number of particles (18 particles in each rectangle). However, the triangle on the left hand side is smaller than the one on the right. This difference in sizes is used to depict different volumes.
Can two objects have the same volume but different densities?
Yes! If two objects have the same volume but different masses, you should expect their densities to be different. Here is a model to illustrate the concept.
As you can see, there are more particles in the rectangle with the blue circles than the rectangle with the green circles. Together, the blue particles have more mass than the green circles. Therefore, whenever you calculate the density of two objects that have the same volume but different mass, you should expect their densities to be different.
Does temperature affect the density of matter?
Yes, temperature affects the density of matter. So in books you sometimes see density values reported along side the temperature at which these values were measured.
How does temperature affect the density of matter?
When the temperature of matter increase, the kinetic energy of its molecules increases as well. This increase in kinetic energy causes the molecules to move much more, increasing the distance between them. For this reason, the volume of the substance increases. Likewise, if the temperature of the subtance decrease, the kinetic energy of its molecules decreases as well. This decrease in kinetic energy cause the molecules to move much less, decreasing the distance between them. For this reason, the volume of the substance shrinks. However, there are
exceptions.
For example, when the temperature of water drops, its volume increase as water turns into ice, decreasing its density. This is so because as water freezes, it forms hexagonal crystal structure. This hexagonal structures contain more spaces within and between them, as a result, the volume of ice increases. This strange behavior of water enables life to thrive in our water bodies during winter. Thus, during winter, as water freezes and turns into ice, it becomes less dense than the surrounding water and so it floats in liquid water. As the ice floats, it shields the liquid water below it from freezing. Thus, providing a suitable environment for aquatic life to thrive.
Popular students’ misconceptions of density
Some popular students’ misconceptions concerning density include:
- Bigger or heavier things sink, while smaller or lighter things float
- Things with air in them float
- Things with holes in them sink