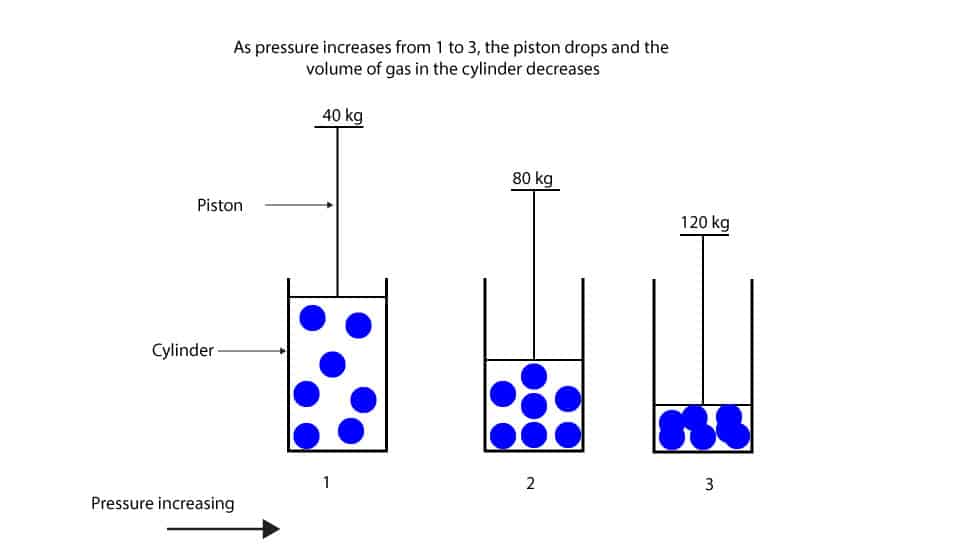
What’s the relationship between pressure and volume of gas?
The pressure (P) of gas is inversely proportional to the volume (V) of gas. This means that as we hold temperature (T) and amount (n) of gas constant (same), as the pressure of gas molecules increase, the volume of gas molecules decrease. Mathematically, we can write this relationship as:
P ∝1/V
If we remove the proportionality sign and introduce an equal sign and a proportionality constant, we will get:
P = K/V
If we multiply both sides of the equation by V, we will get the expression: PV = K.
Notice that we have held the temperature (T) and amount of gas (n) constant.
Since P times (x) V is equal to a constant: K, then it follows that different conditions of pressure and volume for the same mass of gas at constant temperature can be expressed as:
P1V1 =K= P2V2, thus, P1V1= P2V2, equation (1)
where;
- P1 = old pressure
- V1 = old volume
- P2 = new pressure
- V2 = new volume
Basically, if you know three of the four variables in equation 1, you can solve for the fourth variable. However, you must make sure your units agree with each other. That is V1 & V2 should be in the same units and P1 and P2 should also be in the same units.
How to use equation 1 to calculate gas volume or pressure
At constant temperature of 35 ºC, a sample of gas occupies a volume of 5.0 L and has a pressure of 2 atm. If the volume of the gas decreased to 2.0 L, calculate its new pressure.
Answer
Let’s use the following models to make sense of the problem
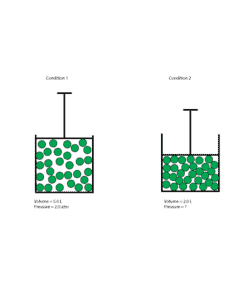
Clearly, from the model you can see that as the volume of gas decreased, its molecules become more crowded and collide more often with the walls of the container. As a result, the new pressure inside the container should be higher than the old pressure.
Therefore,
V1, old volume = 5.0 L
P1, old pressure = 2 atm
V2, new volume = 2.0 L
P2, new pressure = ?
Since P1V1 = P2V2, then it follows that;
5.0 L x 2 atm = 2.0 L x P2
If you isolate P2 by dividing the left and right sides of the equal sign, you will get:
P2 = (5.0 L x 2.0 atm)/2.0 L = 5.0 atm.
Hence, the new pressure is 5.0 atm. This new pressure is higher than the old one and agrees with our initial prediction.
How do Graphs of pressure versus volume look?
The relationship between pressure and volume (P-V relationship) is usually called Boyle’s law in honor of Robert Boyle, who was first to uncover the relationship.
If you plot pressure versus volume or pressure versus inverse of volume (1/v), you will get graphs like the ones in this model.
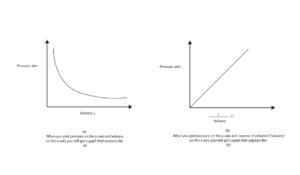
Where can we apply Boyle’s law?
Anytime we breathe, we apply Boyle’s law. To breathe in, we must expand our rib cage to increase its volume so that the pressure inside our lungs can decrease. Once the pressure inside our lungs becomes lower than the atmospheric pressure, air molecules are able to rush in through our nostrils. Similarly, to breathe out, we must contract our rib cage to decrease its volume so that the pressure inside our lungs can become greater. Once the pressure inside our lungs becomes greater than the atmospheric pressure, air molecules are able to rush out through our nostrils.
Now, let’s use the piston-cylinder model to illustrate Boyle’s law

How can you demonstrate Boyle’s law at home?
You can use a syringe to demonstrate the pressure-volume relationship. Draw some air into syringe, then use one hand to close its mouth, while you use the other hand to apply force on the plunger. You will notice that as you apply more force the volume of gas gets smaller and smaller.
To learn more about the relationship between temperature and volume of gas, click here.
To learn more about the properties of gases, click here.
.