Why’s it necessary to define “system and surroundings”?
System and surroundings are necessary because we have no way to directly measure the amount of energy a substance has. This is so because we have no zero energy and no starting point with which to compare energy. However, we can measure changes in energy by measuring changes in temperature of system and surroundings.
What’re system and surroundings?
To measure the amount of energy a substance absorbs or transfers to another, you have to first defined your system and surroundings. The system is the substance you want to investigate and everything else that surrounds it is the surroundings. For example, imagine that you want to determine the amount of energy you will transfer after an intensive workout to cold water in a bathtub. In this case, you will be the system and water the surroundings. And because your temperature is higher than that of the cold water, you will transfer energy to the cold water as a result of the temperature difference.
How to derive the mathematical formula to measure the amount of energy
From experience, if a gas burner burns at a steady rate (system), it follows that it will transfer energy in equal amounts to heat any substance(surroundings) you put on the burner. Now, imagine that your burner heats two identical kettles: one completely filled and the other half-filled with water. If you stick a thermometer into these kettles, you will realize that the temperature of water rises consistently from its initial temperature to its boiling point. You will also realize that it takes longer and more energy to heat the filled kettle (more mass) than it takes to heat the half-filled kettle (less mass).
What does these observations tell us?
They tell us two things:
First;
- the more mass there is, the more energy a substance will absorb in order to heat up. Thus, the amount of energy absorbed is proportional to mass
Second;
- the more energy a substance absorbs, the higher its temperature change. Thus, the amount of energy absorbed is proportional to temperature change
Therefore, if we represent the amount of energy absorbed or released as q, the mass as m, and the temperature change as ∆T. Then we can write a mathematical expression as: q ∞m∆T. If we remove the proportionality sign(∞) and introduce an equal sign and constant Cs, then we will get: q = Csm∆T. Thus,
q = amount of energy absorbed or released by a substance
m = mass
Cs = specific heat capacity
∆T = change in temperature
To get ∆T, you must subtract initial temperature from final temperature. This means that ∆T can be negative or positive.
Therefore, to calculate the amount of energy absorbed or released by a substance, here is the formula to use: q = Cs x m x ∆T.
What’s specific heat capacity, Cs?
Specific heat capacity is the amount of energy needed to raise the temperature of one gram of substance one degree Celsius. Let’s use the data in the following table to see how specific heat capacity vary across different materials.
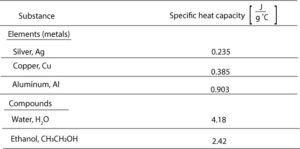
From the table, you can see that
- Metals have lower specific heat capacities. This means that it takes little energy to heat 1 g of metal and have its temperature go up by 1 °C. For example, it takes 0.235 J of energy to heat 1 g of silver and have its temperature go up by 1 °C.
- Water and ethanol have higher specific heat capacities. This means that it takes much energy to heat 1 g of water or 1 g of ethanol and have its temperature go up by 1 ° This is why water stores and absorbs energy so well.
In real life, how can we take advantage of how things absorb energy?
Here are few:
- We generally use metals to make our cooking utensils so that our food can cook well and faster
- We usually use water to fill our car radiators so that our car engines can cool well and faster
To read about energy, click here.