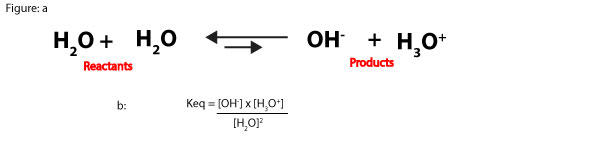
What’s the concentration of water molecules in water?
Pure water has a concentration of 55.6 M. Meaning there are 55.6 moles of water
{(1000 g x (1 mol/18 g)} of water) in 1 liter of water.
Where from the 55.6 M?
The density of water is about 1 gram per milliliters (1 g/mL). Therefore, it follows that 1000 mL (one liter) of water will contain 1000 g of water molecules. And since the molar mass of water is 18 g per mol (18 g/mol), we can convert the 1000 g of water to moles of water by multiplying 1000 g of water by the ratio (1 mol/18 g). Thus,
1000 g x (1 mol/18 g) = 55.6 mol.
Since Molarity is concentration expressed in moles per liter, we just have to divide the 55.6 mol by 1 L to get 55.6 M.
As you can see, this number is so large that we can dissolve chemicals in water without changing its concentration that much. For this reason, when an aqueous solution is dilute, the concentration of water is relatively constant. Because of this, we can multiply the reactants concentration, [H2O]2 by the equilibrium constant, Keq in the following equilibrium expression:
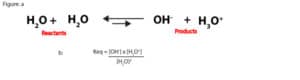
to form a new equilibrium constant, Kwater (Kw). Kw is usually called the ion-product constant of water, and it’s derived as:
Keq[H2O]2 = Kw = [OH–] x [H3O+]
Kw = [OH–] x [H3O+]
What this expression tells us is that we can change the concentrations of the hydronium and hydroxide ions in water by adding an acid or base to it.
Since we know that one liter of pure water at 25°C contains 1.0 x 10-7 moles of hydronium(H3O+) ions per liter of pure water and exactly the same number of hydroxide (OH–) ions, we can calculate the value of Kw.
Thus, Kw = [OH–] x [H3O+] = [10-7 M] x [10-7 M] = 10-14
Notice that Kw has no units. And as long as temperature stays constant at 25°C, the value of Kw will always be equal to 10-14.