What’s the pH concept?
The pH concept was developed to make it easier to report “hydrogen ion” concentration in solution. For example, it is tedious to keep saying that the concentration of hydrogen ion– [H+] —in water at 25 °C is 0.0000001 moles per liter. If this same value is written in standard notation, we will get 10-7moles per liter. From the value 10-7, why can’t we simply get rid of the 10 and the negative, and then say the solution’s pH is 7? That is where the pH concept comes in.
So, what is pH(small p, capital H)?
The small p can be interpreted as “the negative logarithm of”, while the H can be interpreted as “hydrogen ion” concentration. Therefore, pH is defined as the negative logarithm to the base 10 of hydrogen ion concentration in moles per liter. Mathematically, we can express this relationship as:

As you can see, the pH is now defined as the negative log to the base 10 of hydrogen ion concentration. However, these hydrogen ions (H+) are so reactive that they do not stay in solution as “naked” hydrogen ions. Rather, they attach themselves to water molecules to form the hydronium ion. These hydronium ions are usually represented chemically as: H3O+.
What does log to the base 10 mean?
It means a power or exponent of 10. That is when you enter log 1000 in your calculator, you are actually asking your calculator to what power or exponent must you raise 10 to get the number 1000. If you punched in log 1000 correctly, your calculator should spit out 3. That is log 1000 = 3. So, always remember that a log to the base 10 of a number usually means to what power or exponent must you raise 10, to get that number. The power or exponent you get is the log of that number. Now let’s work some examples:
Example
- What is the log of 1.0 x 10-12? Since we know that any number multiplied by 1 is always equal to that same number, then we can simply rewrite the previous question as: what is the log of 10-12?
Solution
With your scientific calculator, punch in log and then 10-12. If you entered it correctly, your calculator should spit out -12.
What is the pH scale and how was it constructed?
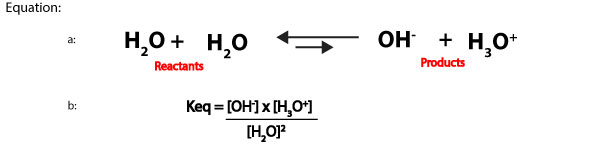
The pH scale consists of pH values. These values are used to determine whether a solution is acidic, basic or neutral. The pH scale was developed by calculating the hydrogen ion concentration in aqueous solution, and then taking the negative log of these values. Now, let’s further explain the previous statement with the following: we know that aqueous solutions usually contain water as the solvent. Water can auto dissociate to produce little amounts of hydrogen ions (hydronium ions) and hydroxide ions. These ions are normally in equilibrium with undissociated water molecules. Which means we can write the auto dissociation of water (equation a) and its equilibrium expression (equation b) as:
When an aqueous solution is dilute, the concentration of water is relatively constant. This means from the equilibrium expression in equation b above, we can multiply the reactants concentration, [H2O]2 by the equilibrium constant, Keq to form a new equilibrium constant, Kwater, denoted as, Kw. Kw is usually called the ion-product constant of water, and it’s derived by multiplying Keq by [H2O]2. That is:
- Keq[H2O]2 = Kw = [OH–] x [H3O+]. We can rewrite this expression as:
- Kw = [OH–] x [H3O+]
Since we know from conductivity experiments that one liter of pure water at 25°C contains 1.0 x 10-7moles of hydronium(H3O+) ions per liter of pure water and exactly the same number of hydroxide (OH–) ions, we can calculate the value of Kw as:
Kw = [OH–] x [H3O+] = [10-7M] x [10-7M] = 10-14———-(2)
From equation 2, you will notice that:
- Kw has no units, and as long as temperature stays constant at 25°C, the value of Kw will always be equal to 10-14.
- regardless of how acidic or basic a solution might be, it must contain both hydronium and hydroxide ions. And when you multiply their molar concentrations together, you will get a value equal to Kw.
Therefore, from equation 2 above, we can rewrite that:
[OH–][H3O+] = Kw = 10-14—————(3)
If we multiply through equation 3 by negative logarithm (-log), we will get the expression:
-log [OH–][H3O+] = -log Kw = -log 10-14—————(4)
From the laws of logarithms, when you take the log of two numbers multiplied by each other, the result is always equal to the sum of the logarithms of the two numbers.
That is: log ab = log a + log b
Because of this, we can rewrite equation 4 as:
(-log [OH–]) + (-log[H3O+]) = (-log Kw)= (-log 10-14) ———(5)
but, logkw= pKw, pOH = -log [OH–], pH = -log [H3O+], and -log10-14= 14. Therefore, we can rewrite equation 5 as:
pOH + pH = pKw = 14 ————-(6)
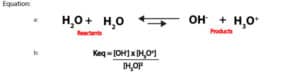
The relationship between the molar concentration of [H3O+] and [OH–] or pH and pOH of an aqueous solution can be illustrated by a simple diagram called the pH scale. This scale is shown in figure 3 below:
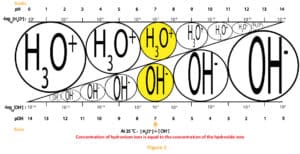
As you can see, the pH values run from 0 to 14. pH values below 7 means the solution is acidic, pH values above 7 means the solution is basic, and pH exactly 7 means the solution is neutral. For highly acidic solutions, pH values can fall below 0, and for highly basic solutions, pH values can rise above 14. Further, you will realize that we have exaggerated the pH scale above to show the differing levels of the hydronium and hydroxide ions concentration as you move from left to right or right to left.
Typically, pH is used for reporting both acidity and basicity. However, a second scale based on pOH could also be used. We have shown the pOH values at the base of figure 3.
From the scale, you can see that H3O+and OH–ions must always be in equilibrium. And at pH of 7, the concentration of the hydronium and hydroxide ions are equal. However, as the concentration of the hydronium ion increase, the concentration of the hydroxide ions must decrease. And as the concentration of hydroxide ions increase, the concentration of the hydronium ions must decrease. That is the two ions exist in tandem and in an inverse relationship. On top of that, the pH scale is logarithmic. Meaning a unit decrease in pH is equivalent to ten times increase in acidity. And a unit increase in pH is equivalent to 10 times decrease in acidity. Let’s further explain this with the following example.
Suppose the pH of an aqueous solution decreases from 2 to 0, then it means that the H3O+concentration increases from 0.02 M (0.02 M x 100) to 2 M, 100 times increase in acidity. That is a decrease of 2 pH units is equivalent to 100 times (10 x 10) increase in acidity.
How can pH be measured?
If you know a solution’s concentration of hydronium ions, you can easily calculate its pH. However, if you don’t know a solution’s concentration of hydronium ions, you can determine its pH by experiment. At least, two methods are widely used to determine solution pH. One requires the use of color indicator solutions, while the other requires the use of pH meter.
What are color indicators?
Color indicators are organic dyes. Dyes are usually weak acids or bases that can change color in acidic and basic solutions. Examples of color indicators include:
- blue litmus
- red litmus
These dyes are usually coated on paper and called:
- red litmus paper
- blue litmus paper
Acids usually turn blue litmus paper red, while bases turn red litmus paper blue.
Many color indicators exist, and they vary widely in the colors they display in acidic and basic solutions.
To determine the pH of solution using an indicator universal paper, you must compare the color of sample plus indicator to the colors on the indicator’s pH scale. Here is an example of such a scale:
What is a pH meter?
A pH meter usually consists of a pair of electrodes. One of these electrodes is sensitive to pH, while the other maintains a constant voltage. Usually you insert these electrodes into your solution and the meter spits out the solution’s pH.