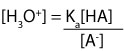How do you calculate the pH of a buffer solution?

How do you calculate the pH of a buffer solution?

You can calculate the pH of buffer solution in two ways. First, you can use the acid dissociation constant expression, and second you can use the Henderson-Hasselbalch equation. But first, let’s use the acid dissociation constant equation to explain how to calculate the pH of buffer solution:

How to use the acid dissociation constant expression to calculate the pH of buffer

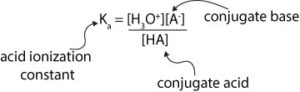
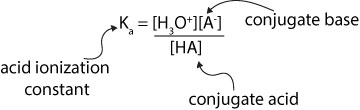
From the expression, the equilibrium concentrations of the hydronium ion and the conjugate base appear in the numerator (top of expression), while the equilibrium concentration of the undissociated conjugate acid appear in the denominator (bottom of expression).

To use the above expression to calculate the pH of buffer, you must know the:

• value of K_a,
• concentration of the conjugate acid and
• concentration of the conjugate base

Once you calculate the concentration of the hydronium ion(H₃O⁺), you will then move on to take the negative log of the hydronium ion concentration (-log[H₃O⁺]) to get the pH of the buffer.

Now, let’s apply our understanding to calculate the pH of the buffer solution in the following example.

Example

Assume that you prepared a 1.000 L of buffer solution by adding 0.0035 mol of carbonic acid to 0.035 mol hydrogen carbonate ion, what is the pH of the buffer solution. Note that the K_a of carbonic acid is 4.2 x 10^-7.

Strategy

Since from the question, we know that the

• K_a of carbonic acid: 4.2 x 10^-7
• concentration of carbonic acid: 0.035 mol/L (divided by 1.000 L to get concentration)
• concentration of hydrogen carbonate ion: 0.0035 mol/L

We can use the acid dissociation constant equation to calculate hydronium ion concentration and then use -log [H₃O⁺] to calculate the pH of buffer. But first, here is the balanced equation and dissociation constant expression for carbonic acid:

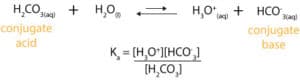
Next, let’s use the following reaction table to track changes in concentration of reactants and products as the reaction occurs.

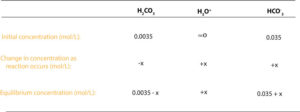
From the table notice that before the reaction starts, we have 0.0035 mol/L carbonic acid, 0.035 mol/L hydrogen carbonate ion and about zero mol/L hydronium ion. As soon as the reaction begins, the concentration of the carbonic acid starts to decrease, while the concentration of the hydronium and hydrogen carbonate ion starts to increase by the same amount. The H₃O⁺and HCO₃^–concentration increases because each H₂CO₃ that dissociates produces one H₃O⁺and one HCO₃^–. For this reason, we have used minus x to represent the concentration of carbonic acid molecules that disappear and plus x to represent the concentration of hydronium ions and hydrogen carbonate ions that appear in the reaction.

Notice that because the K_a value of carbonic acid is so small, we can safely assume that carbonic acid dissociates so little. As a result, the equilibrium concentration of carbonic acid is about 0.0035—(0.0035 -x ≈ 0.0035). And the equilibrium concentration of the hydrogen carbonate ion is about 0.035—(0.035 + x ≈ 0.035). These values can then be substituted into the K_a expression to calculate the concentration of H₃O⁺ as shown in the following example.

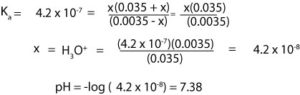
From the calculation above, the pH of buffer solution is 7.38. Now, let’s check our answer to see whether it’s reasonable. For instance, if the concentration of HCO₃^–was equal to the concentration of H₂CO₃, then the concentration of H₃O⁺ will be equal to the acid dissociation constant, K_a. However, this was not the case, because the concentration of the conjugate base (HCO₃^–) was ten times more than the concentration of the conjugate acid (H₂CO₃). This means as we divide a smaller concentration value by a larger one, we should expect the concentration of H₃O⁺ to be less than the K_a. From our calculation, the concentration of H₃O⁺ was indeed less than K_a,therefore, we can say that our answer was reasonable.

How to calculate the pH of buffer using the Henderson-Hasselbalch equation

To use the Henderson-Hasselbalch equation to calculate the pH of buffer, you must know the concentration of:

• conjugate acid
• conjugate base
• pK_a

But first, where did the Henderson-Hasselbalch come from?

The Henderson-Hasselbalch equation is derived from the acid dissociation constant expression for a weak acid. Here is the expression:

where [HA] represents the concentration of weak acid, [A^–] the concentration of the conjugate base, and [H₃O⁺] the concentration of the hydronium ion.

Now, let’s express the equation in terms of [H₃O⁺]. To do this, we must first multiply both sides of the equation by [HA] and then divide both sides by [A^–]. If we do, our expression will appear like this:

Next, we convert the [H₃O⁺] to pH. To accomplish this, we take the base 10 logarithm of each side of the above equation. If we do, we will get:

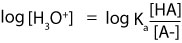
However, from a law in logarithm, logAB is the same as writing logA + logB. Since K_a is multiplied by the ratio [HA]/[A^–], then it means that we can rewrite the previous expression as:

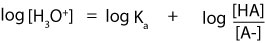
Next, to convert [H₃O⁺] to pH we must multiply both sides of the equation by negative 1 (-1). If we do, the previous expression becomes:

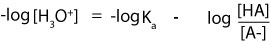
However, -log[H₃O⁺] is the same as pH, -logK_a is the same as pK_a, and – log [HA]/[A^–] becomes +log[A-]/[HA]. Note that in the new expression: +log[A-]/[HA], the negative sign has changed to positive and the acid and conjugate base have switched places. Finally, the Henderson-Hasselbalch is:

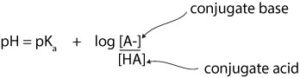
Now let’s apply Henderson-Hasselbalch to solve the same example we solved earlier using the acid dissociation constant. Here is the same question:

Example

Assume that you prepared a 1.000 L of buffer solution by adding 0.0035 mol of carbonic acid to 0.035 mol hydrogen carbonate ion, what is the pH of the buffer solution. Note that the K_a of carbonic acid is 4.2 x 10^-7.

Solution

The Henderson-Hasselbalch is:

Since

• K_a of carbonic acid: 4.2 x 10^-7and pK_a = -logK_a,which is equal to -log (4.2 x10^-7)
• concentration of carbonic acid: 0.035 mol/L (divided by 1.000 L to get concentration)
• concentration of hydrogen carbonate ion: 0.0035 mol/L

Therefore,

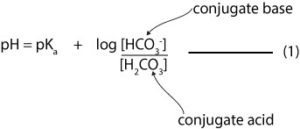
If we substitute the values in equation 1 above, we will get:

pH = -log (4.2 x 10^-7)+ log (0.035/0.0035)

pH = 6.38 + 1 = 7.38

Therefore, the pH of the buffer solution is 7.38. This answer is the same one we got using the acid dissociation constant expression.

Here we have used the Henderson-Hasselbalch to calculate the pH of buffer solution. In addition to that, we can also use the Henderson-Hasselbalch equation to calculate the ratio of the concentration of conjugate base to the concentration of conjugate acid needed to prepare a buffer of a particular concentration.

What is buffer range and at what range is it most effective?

Buffer range is the pH range over which the buffer is most effective. This range is usually between 0.1 and 10. In practice, when the [A^–]/[HA] ratio is less than 0.1 or when the concentration of one component is more than 10 times as concentrated as the other, buffering capacity is weak.