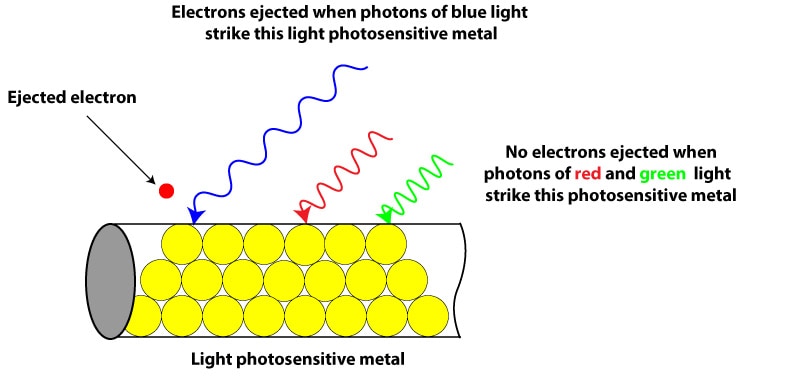
Back then (in the 1900s) scientists saw that when light of certain frequency and energy shines on a light sensitive (photosensitive) metal, the metal emitted electrons, generating an electric current as a result (photoelectric effect). They also observed that light had a threshold (limit) frequency below which no electrons could be ejected. For instance, from the electromagnetic spectrum, blue light has more energy than yellow light. If a photosensitive metal requires photons of blue light to emit electrons, photons of green, yellow, and other light of lower frequency won’t transfer enough energy to allow electrons break the attractive forces holding them to the metal.
Yet, no one back then could explain the causes behind the photoelectric effect. But that changed when Albert Einstein came along and applied Max Planck’s idea of quanta to explain the photoelectric effect. Einstein assumed that Planck’s “quantum’ consists of massless particles. Einstein called these massless particles photons, and he believed that light was a stream of photons, and these photons exhibited both particle-like and wave-like properties (particle-wave duality of light). As a result, when a photon with the right frequency and energy (E = hν) strikes an electron on a light sensitive metal, the photon transfers its energy to the electron, once the electron absorbs this energy, it uses some to break the attractive forces holding it to the metal, and some to increase its kinetic energy so that it can eject itself from the metal surface.
If we represent the energy of the bound electron as W = hνo, where νo is the threshold frequency. It means that only light (photons) with energy greater than W will eject electrons from photosensitive metals. The excess energy as a result of the ejection is converted to kinetic energy of the ejected electron. Mathematically, we can write a relationship using the energy of the photon (E = hν), the energy of the bound electron (W = hνo), and the kinetic energy (KE) of the ejected electron as:
KEelectron= hν- hνo
Where;
h is Planck’s constant
ν is frequency
νo is threshold frequency
Kinetic energy (KE) = ½ mv2, where m is mass, and v is velocity