In combustion analysis, we usually burn an organic compound in oxygen to convert the carbon in the compound to carbon dioxide and the hydrogen to water. The carbon dioxide produced as a result of the burning is absorbed by sodium hydroxide. While the water produced as a result of the burning is absorbed by magnesium perchlorate. Once the burning is complete, we weigh the carbon dioxide absorber and the water absorber. To determine the mass of water, we subtract the mass of the water absorber before burning from the mass of the water absorber after burning. To determine the mass of carbon dioxide, we subtract the mass of the CO2 absorber before burning from the mass of the CO2 absorber after burning. Next, we use the mass of carbon dioxide to calculate the mass of carbon in the original compound and the mass of water to calculate the mass of hydrogen in the original compound. Here is a simplified illustration of the instrument used in combustion analysis:
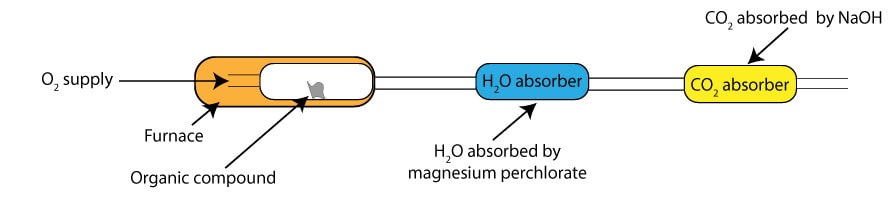
As you can see, the instrument has three separate compartments that are all connected to one another. The first compartment is the furnace, where you burn your sample to generate carbon dioxide and water. These chemicals then travel to the second compartment, where water is absorbed, and into the third compartment where carbon dioxide is absorbed.
Now, imagine that we burned an organic compound that also contained oxygen. How would we determine the mass of oxygen?
To determine the mass of oxygen, we will subtract the combined masses of carbon and hydrogen from the mass of our compound (sample). That is:
mass of oxygen = mass of sample – (mass of carbon plus mass of hydrogen)
Now, let’s use the following combustion analysis results to determine the empirical formula of an organic compound.
Imagine that we have an organic compound that contains C, H, and O. If we burn 1.00 g of this compound to produce 1.50 g of CO2 and 0.41 g of H2O, what is the empirical formula of the compound.
Solution
To determine the empirical formula of this compound, we must first calculate the masses of C, H, and O.
To calculate the mass of carbon, we must convert the mass of CO2 to the mass of carbon. Here is how to do it:
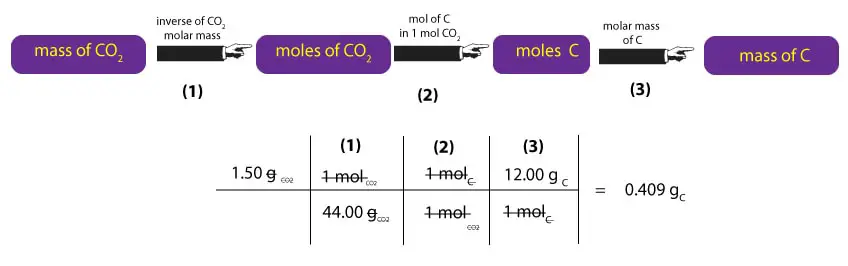
As you can see, to convert mass of CO2 to mass of C, we must first multiply the mass of CO2 by the inverse of its molar mass. This calculation is shown in step (1) above. Once we have moles of CO2, we must convert moles of CO2 to moles of C. To do this, we must remember that 1 mole of CO2 contains 1 mole of carbon and 2 moles of oxygen. Where from the 1 and 2? We just read the subscripts of C and O in C1O2 as moles. That is, one molecule of CO2 contains 1 atom of carbon and 2 atoms of oxygen. As a result, we can say that one mole of CO2, will always contain 1 mole of C and 2 moles of CO2. But since we are interested in carbon, we ignore the oxygen. Therefore, to convert moles of CO2 to moles of C, we must multiply moles of CO2 by the ratio 1 mol C/1 mol CO2. This calculation is shown in step (2) above. Once we get the moles of C, we will then multiply it by its corresponding molar mass to convert moles of C to mass of C in grams. This calculation is shown in step (3) above.
Similarly, to convert mass of H2O to mass of H, we must first multiply the mass of H2O by the inverse of its molar mass. This calculation is shown in step (1) below. Once we have moles of H2O, we must convert moles of H2O to moles of H. To do this, we must remember that 1 mole of H2O contains 2 moles of hydrogen and 1 mole of oxygen. Where from the 2 and 1? We just read the subscripts of H and O in H2O1 as moles. That is, one molecule H2O contains 2 atoms of hydrogen and 1 atom of oxygen. As a result, we can say that one mole of H2O, will always contain 2 moles of H and 1 mole of O. But since we are interested in hydrogen, we ignore the oxygen. Therefore, to convert moles of H2O to moles of H, we must multiply moles of H2O by the ratio 2 mol H/1 mol H2O. This calculation is shown in step (2) below. Once we get the moles of H, we will then multiply it by its corresponding molar mass to convert moles of H to mass of H in grams. This calculation is shown in step (3) below.
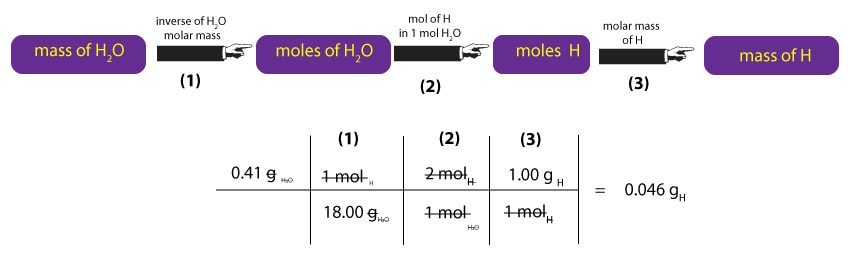
So, as a result of our calculations, we now know that the mass of carbon is 0.409 g and the mass of H is 0.046 g. But since our compound also contains oxygen, we must determine the mass of oxygen too. To do this, we must recall that:
mass of oxygen = mass of sample – (mass of carbon plus mass of hydrogen)
Since we burned 1.00 g of our sample, it follows that we can calculate the mass of oxygen by subtracting the combined masses of C and O from the mass of sample. That is:
mass of oxygen = 1.00 g – (0.409 g + 0.046 g) = 1.00 g – 0.455 g = 0.545 g.
Thus, the masses of C, H, and O are:
C = 0.409 g
H = 0.046 g
O = 0.545 g
Now, just like we did before, we must convert the mass of each element to moles by multiplying by the inverse of its corresponding molar mass. That is,
for carbon, we will do:
0.409 g x 1 mol/12.00 g = 0.03408 mol
for hydrogen, we will do:
0.046 g x 1 mol/1.01 g = 0.04554 mol
for oxygen, we will do:
0.545 g x 1 mol/16.00 g = 0.03406 mol
Next, we will find the mole ratio of the elements in the compound by dividing through by the smallest moles. As you can see, oxygen has the smallest moles. Therefore, we will do:
0.03408 mol C/0.03406 mol O = 1.000 C/1.000 O
0.04554 mol H/0.03406 mol O = 1.337 H/1.000 O
0.03406 mol O/0.03406 mol O = 1.000 O/1.000 O
From above, the ratios are: 1.000 mol C; 1.337 mol H, and 1.00 mol O. Since there are no partial atoms, we must multiply the ratios by a number to covert the 1.337 to the nearest whole number. After scratching my head and guessing many times, I noticed 3 will do. So, when we multiply through by 3, we will get: 1.000 mol C x 3 = 3.000 mol C
1.337 mol H x 3 = 4.011 mol H
1.000 mol O x 3 = 3.000 mol O.
Thus, the new ratios are:
3.000 mol C; 4.011 mol H; and 3.000 mol O
As a result, when we take these ratios into account, the empirical formula of our organic compound is: C3H4O3
Now, imagine that in another experiment we determined the molar mass of this compound to be 176.00 g/mol. What then is its molecular formula? To determine the molecular formula, we must remember that empirical formula multiplied by a certain number, n, will give the molecular formula. We can write this relationship as:
(Empirical formula) n = Molecular formula.
We can also write the above equation in another way as:
(Molar mass of empirical formula) n = Molar mass of molecular formula
Since the empirical formula of our compound is C3H4O3, it follows that its empirical formula molar mass is: (3 x 12.00g/mol) + (4 x 1.00 g/mol) + (3 x 16.00 g/mol) = 36.00 g/mol + 4.00 g/mol + 48.00 g/mol = 88.00 g/mol.
Next, we can write that:
(88.00 g/mol) n= 176.00 g/mol
Therefore,
n = 176.00/88.00 = 2. Since we now know n = 2, we can write that:
(C3H4O3)2 = Molecular formula. If we multiply all the subscripts in the empirical formula by 2, then our molecular formula will be: C6H8O6. From this formula we can say that our organic compound is vitamin C.
Notice that, n can have values from 1, 2, 3 and so on. When n = 1, it usually means that the empirical formula is the same as the molecular formula.
If you want to learn how to determine empirical formula from percentage composition click here.