The van der Waal equation was developed to address the limitations of the ideal gas equation. Recall that the ideal gas equation is usually written as: PV = nRT, and the van der Waal’s equation as:
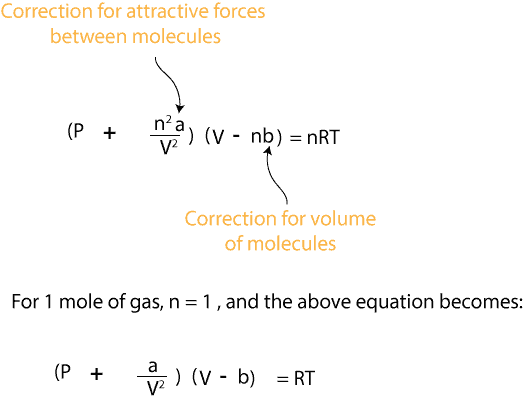
where the variable b, is a constant and relates to the actual volume of the gas molecules themselves, and a, is a constant and relates to the strength of the attractive forces between gas molecules. Together, the variable a/V2represents the correction factor for the pressure due to the attractive forces between gas molecules, while the variable (V-b) represents the correction factor for the volume due to the actual volume of the gas molecules themselves.
What are the limitations of the ideal gas equation (ideal gas law)?
An ideal gas is a gas that behaves exactly as that predicted by the ideal gas equation. However, in real life, we have only real gases, and the behavior of real gases is much more complex than an ideal gas. As a result, the ideal gas equation is inaccurate when used to predict the exact behavior of real gases under unusual conditions such as increasing pressures and decreasing temperatures.
And the reason why is inaccurate is because of the assumptions in the kinetic-molecular theory (KMT) of gases. As you recall, the ideal gas equation was developed based on the kinetic-molecular theory KMT) of gases. And assumptions of the KMT include:
- Gas molecules are much smaller than the distances between them. Because of this, the actual volume of gas molecules can be ignored
- Gas molecules are in constant random motion, colliding with themselves and the walls of their container to generate pressure. Because of this behavior, gas molecules do not attract one another.
When do the above assumptions breakdown?
In real life, when a real gas is compressed, the assumptions of the ideal gas law break down under the conditions of increasing pressure and decreasing temperature. To make sense of this, let’s turn to the following graph to see how increasing pressure and decreasing temperature affect the molar volume of gas as it is compressed.
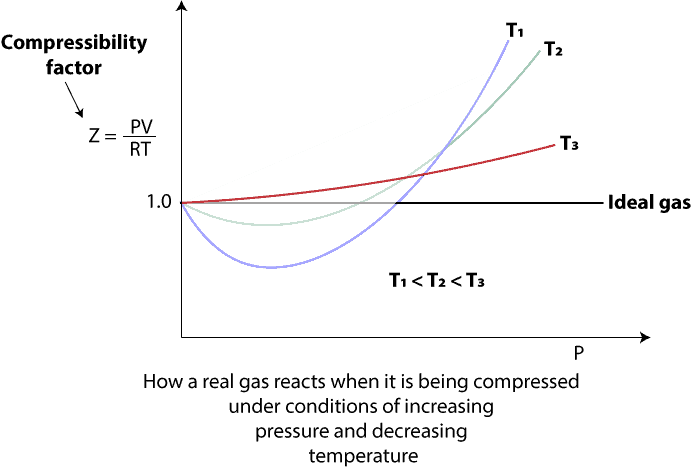
As you can see, the y-axis of the graph represents the compressibility factor, Z for 1 mole of gas, while the x-axis represents the pressure, P. For an ideal gas, which of course obeys the ideal gas equation at all times, we expect that its compressibility factor remains the same (constant) and independent of temperature and pressure. And we represent the compressibility factor of an ideal gas as 1 on the graph above. However, when a real gas at different temperatures (T1, T2, and T3) is subjected to increasing pressure, you will notice some portions of the compressibility curve are greater than 1, while some portions are less than 1. When portions of the curve are greater than 1 at higher pressures, it usually means that the actual volume of the gas molecules is greater than that predicted by the ideal gas equation, and that the molecules are resisting compression. On the other hand, when portions of the compressibility curve are less than 1 at lower pressures, it usually means that the actual volume of the gas molecules is less than that predicted by the ideal gas equation, and that these molecules are not resisting compression as much as an ideal gas would. Because of this, the pressure the real gas exerts on the walls of the container is less than expected. The reason is less than expected is that as external pressure increases and pushes the gas molecules closer together, the attraction between them becomes stronger. And as the attraction becomes stronger, gas molecules move slower and strike the walls of their container with less force.
As a result of the fact that the ideal gas equation cannot correctly predict the behavior of gas molecules at all temperatures and pressures suggests that the actual volume of the gas molecules and the attractive forces between them cannot be simply ignored.
To account for these factors, van der Waal proposed two correction factors to the ideal gas equation. One correction factor took into account the attractive forces between gas molecules (a/V2), while the other took in to account the actual volume of the gas molecules (V-b). When these corrections are added to the ideal gas equation, we generate a new equation called the van der Waal’s equation, and this equation is expressed as:
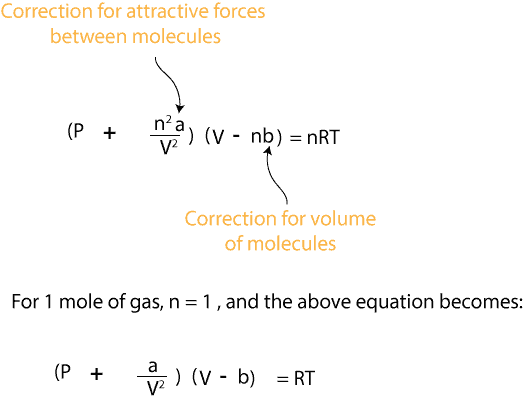
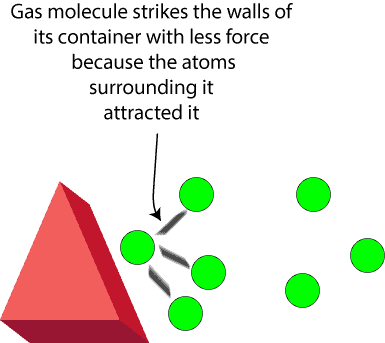
Notice, why is the correction factor due to the attraction between gas molecules not subtracted but added to the pressure, P?
This is added because the attractive forces between gas molecules will reduce the force with which gas molecules would otherwise have collided with the walls of the container. And as the force reduces, the pressure exerted by a real gas is less than that predicted by the ideal gas equation. Because of this, the correction factor is added to account for the reduced pressure. One way to think about this is to picture in your mind a gas molecule on a collision course with the walls of its container but was suddenly attracted by other gas molecules near the wall. Here is an illustration to reinforce your picture:
On the other hand, why is the correction factor due to the actual volume of the gas molecules subtracted but not added to the total volume?
If we consider the total volume of a gas to consists of the spaces occupied by the gas molecules and the empty spaces between them, then it is reasonable to say that when a gas is compressed, it is the empty spaces between gas molecules that become smaller. However, the actual volume occupied by the gas molecules remains unchanged. As a result of this, we must subtract the actual volume of the gas molecules (b) from the total volume (V). But it turns out that the constant b, is actually larger than the actual volume of the gas molecules. This is because when molecules collide, the orientation of the molecules naturally restricts the molecules from entering into some spaces surrounding them. For instance, consider the following two spheres as gas molecules colliding with each other.

As they collide, you will notice that sphere A is restricted from entering the spaces depicted by the dotted circle around sphere B. As you can see, the excluded spaces surrounding both spheres surpass the space occupied by the spheres themselves. Because of this, the correction factor, b in the van der Waal’s equation is more about the excluded space than it is about the actual volume of the gas molecules.
From this, we can say that the van der Waal’s equation is not perfect, but it is still an improved model of the ideal gas equation to predict the behavior of real gases.
To learn more about the kinetic theory of gases, click here and about the ideal gas equation, click here.