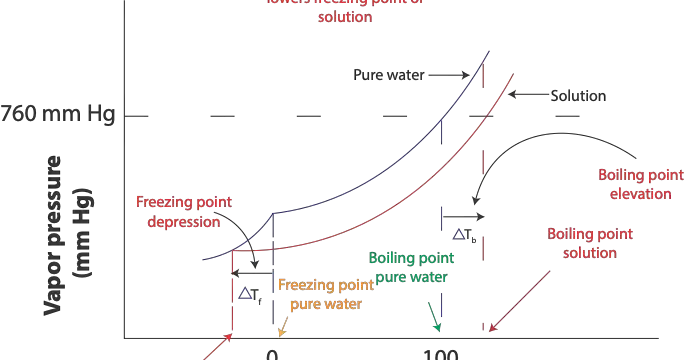
When the vapor pressure of pure water is equal to standard atmospheric pressure (1 atm or 760 mm Hg) at 100 ºC pure water will boil at 100 ºC, which is its normal boiling point. However, since the vapor pressure of salt solution is less than 760 mm Hg at 100 ºC, the salt solution will not boil at 100 ºC. However, salt solution will boil at a temperature higher than the 100 ºC. As a result, adding a non-volatile solute to a pure solvent raises its boiling point. As a result, boiling point elevation, denoted by the symbol ΔTb is the difference between the normal boiling point of pure water and the higher boiling point of its solution (salt solution). This boiling point elevation is illustrated in the following graph.
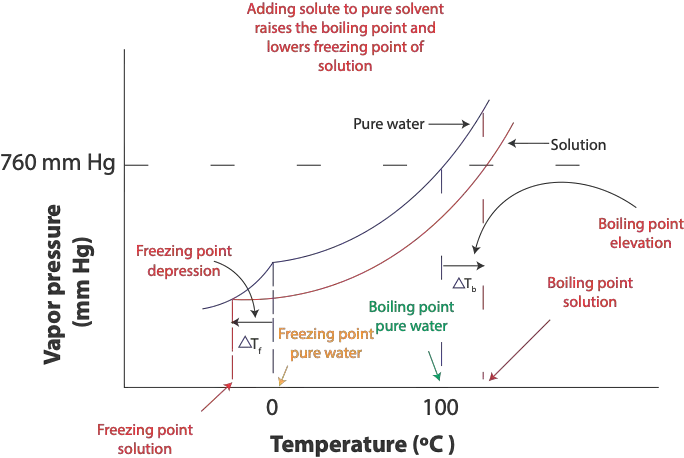
From the diagram, you can see that the freezing point of salt solution, bottom red curve, is lower than the freezing point of pure water. Also, the boiling point of the pure solvent (water) the top curve is 100 ºC at 760 mm Hg, while that of its solution, the bottom curve—salt water is higher than 100 ºC at 760 mm Hg. This increase in boiling point is proportional to the concentration of the solute in Molality. We can calculate this increase in boiling using the formula:
ΔTb = Tb(solution) – Tb (solvent) = Kbmsolute , which we can rewrite as:
ΔTb = = Kbmsolute
Where,
ΔTb is the boiling point of solution minus the boiling point of pure water (solvent)
Kb is the molal boiling point elevation constant of the solvent. For water, its Kb is 0.52 ºC kg/mol.
msolute is the molality of solution. Concentration in Molality is used in the calculation because its value does not change when the temperature changes.
What is freezing point depression?
At the freezing point of pure solvent (water), the attractive forces between the solvent molecules become much stronger such that some molecules in the solvent will gather to form an organized structure in the solid state called a crystal lattice. Once the temperature remains the same, there is a dynamic equilibrium in which the rate at which liquid turns into solid (crystallization) is equal to the rate at which solid turns into liquid (melting). In salt solution, however, the solute particles (sodium and chloride ions) interfere with the attractive forces between the water molecules. This interference slows the rate at which molecules or ions move from solution to solid. Because of this disruption, the freezing point of solution (salt solution) is always lower than the freezing point of the pure solvent (water). This lowering is referred as the freezing point depression, and it is illustrated in the following graph.
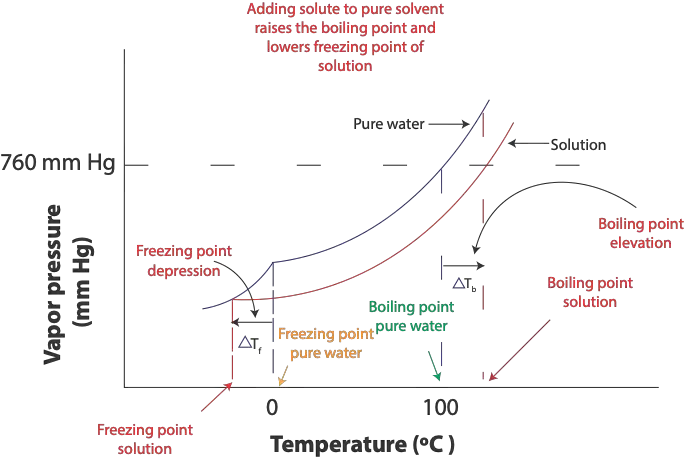
From the diagram, you can see that the freezing point of salt solution, bottom red curve, is lower than the freezing point of pure water (top curve).
This decrease in freezing point is proportional to the concentration of the solute in Molality. We can calculate this decrease in freezing point using the formula:
ΔTf = Tf(solution) – Tf (solvent) = Kf msolute , which we can rewrite as:
ΔTf = Kf msolute
Where,
ΔTf is the freezing point of solution minus the freezing point of pure water (solvent)
Kf is the molal freezing point depression constant of the solvent. For water, its Kf is 1.86 ºC kg/mol.
msolute is the molality of solution. Concentration in Molality is used in the calculation because its value does not change when the temperature changes.
Now, let’s solve the following problem
Calculate the boiling and freezing points of an aqueous solution containing 39.0 g of ethylene glycol (HOCH2CH2OH). dissolved in 760 mL of water. Assume the density of water is 1.0 g/mL, Kb = 0.52 ºC kg/mol and Kf 1.86 ºC kg/mol.
To calculate the boiling point, we must recall that: ΔTb = = Kbmsolute
But since the formula calls for molality, we must convert the 39.0 g of ethylene glycol to moles by dividing by its molar mass. Once we get moles, we will divide it by the mass of water in in Kg to get molality.
To calculate, will do:
39.0g x 1 mol/62.07 g = 0.628 mol ethylene glycol.
Next, we convert 760 mL to grams by using the density of water as a conversion factor. Once we get mass in grams, we divide grams by 1000 to get mass in kg. That is,
760 mL x 1.0 g/mL x 1kg/1000 g = 0.76 kg water
Hence, the molality of the solution, m = 0.628 mol/0.76 kg = 0.826 mol/kg
Next, we calculate the boiling point elevation by plugging our values into the formula
ΔTb = = Kbmsolute
ΔTb = 0.52 ºC kg/mol x 0.826 mol/kg = 0.430 ºC
So, boiling point elevation is 0.430 ºC. Since the normal boiling point of water is 100 ºC, to determine the boiling point of its solution, we will add the 0.430 ºC to 100 ºC to get 100.43 ºC. Therefore, the boiling point of the solution is 100.43 ºC
Similarly, the freezing point lowering is calculated as:
ΔTf = 1.86 ºC kg/mol x 0.826 mol/kg = 1.54 ºC
Therefore, the freezing point depression is 1.54 ºC.
Since water freezes at 0ºC, we will subtract 1.54 ºC from 0 ºC to get the freezing point of solution. Once we do, will get negative -1.54 ºC.
One practical application of freezing point lowering is the salting of roads during winter to remove snow. And from our discussion, since CaCl2 produces 3 ions per formula unit and does release energy during dissolving makes it much suitable for melting icy roads than using NaCl, which produces only 2 ions per formula unit. However, a buildup of CaCl2 and NaCl on roads is toxic to road side plants.
To learn about the colligative property vapor pressure lowering, click here.