A spectrum is the ‘picture’ you get when light interacts with atoms or molecules. A spectrum is usually a plot of how much light is absorbed or emitted versus the wavelength or frequency of light. For example, when white light from the sun or an incandescent light bulb is passed through a glass prism onto a white surface, it separates into a rainbow of colors. This rainbow of colors, called a continuous spectrum, smoothly blends into one another without leaving any gaps in between. They are also the same colors we see within the visible region of the electromagnetic spectrum just like the one below;

On the other hand, when we connect a tube of hydrogen gas (discharge tube of H gas) to a high voltage source and pass the light the gas emits through a glass prism, we usually see only a few colored lines separated by gaps, this spectrum is called a line emission spectrum, and it is similar to the one below;

Each element produces its own unique line spectrum. Because of this, a line emission spectrum is like the “fingerprint” of the element, which we can use to identify the element. So, why do energized hydrogen gas molecules produce a line spectrum but not a continuous spectrum? Bohr had an answer. Bohr assumed that the single electron in a hydrogen atom moved in a path around the nucleus just as planets orbit around the sun.
But then, why doesn’t the electron lose energy at some point in its path and spiral into the nucleus? To account for this, Bohr related the energy of the electron to the radius of the orbit by bringing up Planck’s idea that energy is emitted in packets (quantized). Bohr believed that electrons could only circulate around the nucleus in orbits of certain radii. And that these radii correspond to a specific amount of energy. As a result, the energy of an electron is “quantized” and restricted to certain energy levels. An electron can only move to another energy level if it loses or gains energy equal to the difference in energy between the two levels. Bohr called these energy levels orbits.
If we apply this understanding to our energized tube of hydrogen gas, we can say that as the atoms of hydrogen molecules absorb energy, their electrons become excited (excited state), allowing the electrons jump from a lower energy level to a higher energy level. As they return to their original state (ground state), they emit the extra energy they initially absorbed as light. When this light is passed through a glass prism onto a white surface, we see a few colored lines that fall within the visible region of the electromagnetic spectrum similar to the one below.

As you can see, these colored lines are separated by gaps. To help predict these lines, Bohr developed a mathematical formula. This formula can be expressed as:

where the constant 2.179 x 10-18J, is called the Rydberg constant and n, represents the principal quantum number or energy level. The principal quantum number starts from n = 1 to infinity. Here is an illustration of Bohr’s atomic model;
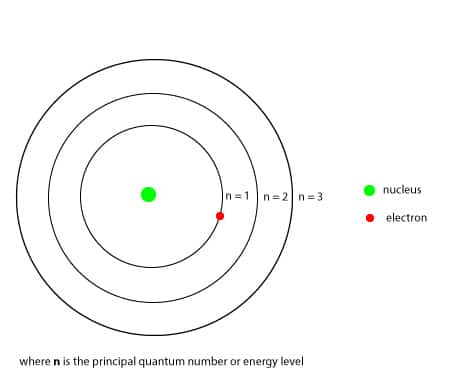
As n gets larger, the size of the orbit and the energy of the electron gets larger as well, but the energy of the electron is restricted to certain energy levels called the principal quantum number, n. And since the n = 1 energy level must be filled before the n = 2, it follows that the single electron of hydrogen will go in the n = 1 energy level as shown above in the Bohr’s atomic model. And because the n = 1 energy level is closer to the nucleus, the negatively charged electron in it will be strongly attracted to the positively charged nucleus, lowering the energy of the electron. Because of this attraction, an electron can move to a higher energy level only if it absorbs energy equal to the difference in energy between the two energy levels. When an electron absorbs energy and moves from a lower energy level to a higher energy level, it is usually referred as moving from the ground state to the excited state. Similarly, when an electron is at an excited state and wants to return to its ground state, it must emit the energy it initially absorbed. This back and forth movement of an electron is called electron transitions. The following is an illustration showing the electron transitions in an excited hydrogen atom;
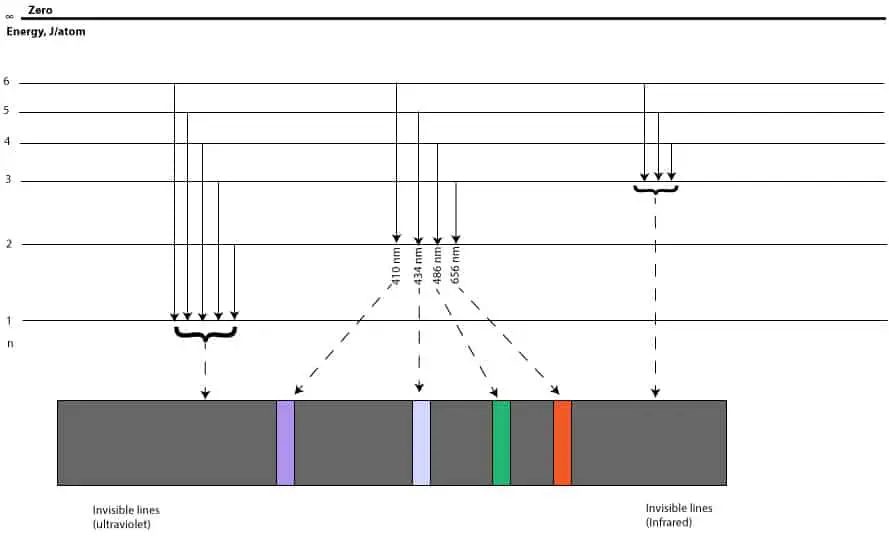
As you can see, electron transitions from n > 1 to n = 1, results in the lines in the ultraviolet region (we can’t see these lines with our eyes). Electron transitions from n > 3 to n = 3, results in lines in the infrared region (we can’t see these lines with our eyes). Electron transitions from n > 2 to n =2, results in the lines within the visible region of the electromagnetic spectrum, we can see these lines with our eyes.
How did Bohr define zero energy?
If you look on the top left side of the above diagram, you will see zero energy. Zero energy refers to the situation in which a sufficiently energized electron breaks its attraction and completely separates itself from the protons in the nucleus. Once an electron attains zero energy, the nucleus will no longer attract it, and the electron will be at a higher potential energy. But once the electron starts to lose energy, its potential energy starts to drop relative to the point at which it had zero energy. Because of this, Bohr’s formula includes a negative sign. This negative sign is attached to the energy values we calculate for an electron in an atom.
Now let’s apply Bohr’s model to calculate the energy of an electron in its ground state (n =1) in a hydrogen atom. To do this, you must recall that:

Since n = 1, it follows that: E = -2.179 x 10-18J (1/12) = -2.179 x 10-18J
When an electron moves from its initial state, Einitial to a final state, Efinal, the difference in energy, ∆E can be calculated as: ∆E = Efinal– Einitial.
When an electron moves from its initial state, Einitial to a final state, Efinal, the difference in energy, ∆E can be calculated as: ∆E = Efinal – Einitial.
When an electron moves from a higher energy level, say n = 4 to a lower energy level, say n = 2, energy is emitted, and ∆E is negative.
When an electron moves from a lower energy level, say n = 1 to a higher energy level, say n = 3, energy is absorbed, and ∆E is positive.
The difference in energy between any two energy levels can be expressed as:

Thus, we can always use equation (2) to calculate the energy difference between any two energy levels. Note that f stands for final, while i stands for initial.
What were the problems of Bohr’s atomic model?
The first was that Bohr’s atomic model could not explain the many lines present in the spectra of elements with more than one electron. These elements include all the elements after hydrogen on the periodic table. Another was that Bohr thought as if there were actually well-defined orbits in an atom. Because of these problems, a new model was needed to explain the line emission spectra of all elements.
An answer came in 1924, when another scientist called Louis de Broglie, suggested that if light can exhibit both particle-like and wave-like properties, then particles of matter such as the electron should also exhibit wave-like properties. De Broglie further proposed an equation describing the wave-like properties of matter. This equation can be expressed mathematically as:
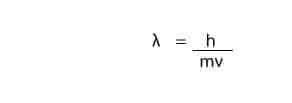
Where;
l: wavelength
h: Planck’s constant
m: mass
v: velocity
Many scientists at first did not accept De Broglie’s hypothesis. However, evidence in support of the hypothesis came in 1927 when scientists working at Bell telephone laboratories observed that atoms in a thin sheet of metal foil diffracted a beam of electrons in the same way that a diffracting gradient diffracts light. From this, it became clear that physicists could now apply the wave equations they had developed for light to describe the wave-like properties of an electron.
A few years after De Broglie’s hypothesis, another scientist called Heisenberg suggested that it was impossible to pinpoint at the same time the exact location and exact momentum of an electron.
Why was it impossible?
Heisenberg believed that the small size of an electron would require that we shine light of shorter wavelength on it in order to see it. But since light of shorter wavelength consists of highly energetic photons. It would mean that when these photons strike a tinny electron by the time the light returns to our eyes the electron would have moved to another location. This difficulty in finding simultaneously the exact location and exact momentum of an electron is referred as the uncertainty principle. As a result of the uncertainty principle, the only way to describe the location of an electron in an atom is to introduce probability into the atomic model.
In 1926, another scientist called Schrodinger did just that. He applied the De Broglie hypothesis to develop a wave equation to describe how an electron behaved within a hydrogen atom. From the wave equation, Schrodinger generated wave functions. These wave functions, which are solutions to the wave equations, are used to predict the energy states of an electron, and the probability of finding it somewhere within an atom.
Although wave functions are abstract mathematical equations that are sometimes hard to understand, we can represent the square of the wave function graphically. These pictures tell us regions within an atom where we are more likely to find an electron with a certain energy.
The region within an atom we are more likely to find an electron is called an orbital. We can represent an orbital by drawing a three-dimensional surface in which we have a higher chance of finding an electron. This higher chance means that in 9 times out of 10 (90%) an electron will likely buzz around somewhere inside this surface (orbital).
Examples of such orbitals, sometimes called electron clouds, include the s and p orbitals, and these orbitals are shown below;
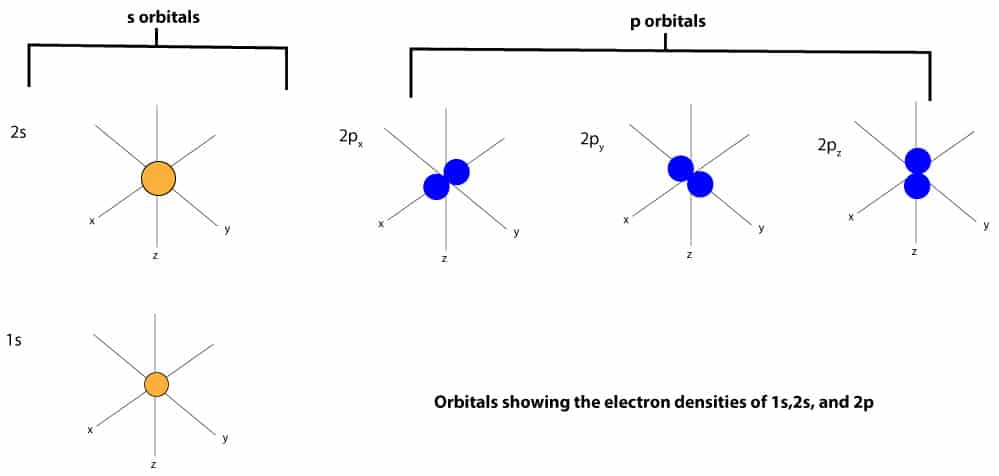
A group of orbtals with the same value of the principal quantum number (n) is called an electron shell. Therefore, from the orbitals above, when n = 1, we get the n = 1 shell, and in this shell, there is only one orbital: the s orbital. When n = 2, we get the n = 2 shell, and in this shell, there are only two orbitals: the s and p orbitals. When we put some of these orbitals together within an atom, we will get something like this:
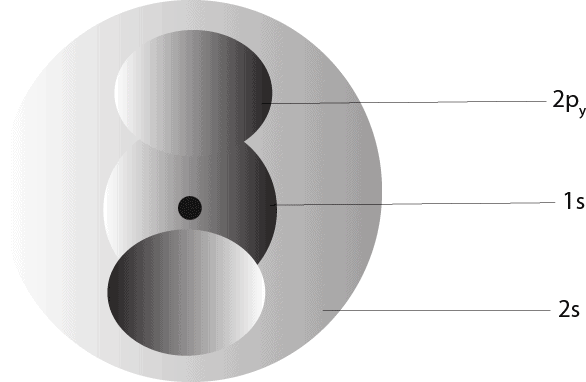
As you can see, the s-orbital is shaped like a sphere, while the p-orbital is shaped like a dumbbell.
Now, how did we arrive at these orbitals, and how can we describe the shape and energy of an electron’s cloud in an atom?
To describe the shape and energy of an electron’s cloud, click here to learn about quantum numbers.