The first quantum number is called the principal quantum number
It is represented by the symbol n. The principal quantum number determines the energy of an electron, and its value, n, corresponds to an energy level called the principal energy level. Values of n starts from n = 1, 2, 3, 4, 5,…. and so on. When an electron is in n = 1, we usually say the electron is in the first principal energy level. When an electron is in n = 2, we usually say the electron is in the second principal energy level and so on. As the value of n increase, the energy of the electron and the distance between the electron and the nucleus also increase. This increase in distance weakens the attraction between the nucleus (holds the positvely charged protons) and the electron.
The second quantum number is called the azimuthal quantum number.
It is represented by the symbol, l, and it describes the shape of the subshells within the principal energy level. A subshell is one or more orbitals with the same principal energy level, n. Values of l starts from 0 to a maximum of n – 1. Thus, values of l will include:
l = 0, 1, 2, 3, to …. (n – 1)
Therefore, if the principal energy level is n = 1, the azimuthal quantum number will be: l = 1 – 1 = 0. The zero here means that the first principal energy level has only one subshell.
If the principal energy level is n = 2, the azimuthal quantum number will be: l = 2 – 1 = 1. When l = 1, values of l will start from l = 0 to l = 1. Thus, the principal energy level will have two subshells: one is l = 0, and the other is l = 1.
If n = 3, then l = 3 – 1 = 2, values of l = 0, 1, 2. This means when n = 3, there are three subshells. The first is l = 0, second is l = 1, and third is l = 2.
To make it easier to recall, we can use letters to represent the values of l(subshells).
If we do this, then when
l = 0; it is referred as the s subshell, where s stands for sharp
l = 1; it is referred as the p subshell, where p stands for principal
l = 2, it is referred as the d subshell, where d stands for diffuse
l = 3, it is referred as the f subshell, where f stands for fundamental
The names of s, p, d, and f were derived from the names of spectral lines.
As you can tell, when atomic orbitals have the same n and l values, they will be in the same subshell. Therefore, to describe the energy and location of a subshell, we must use a number and letter. So, what does the designation 2p mean? It means n = 2 and l = 1. This translates as a p orbital is a subshell of the second principal energy level.
The third quantum number is called the magnetic quantum number.
It is represented by the symbol, ml, and it describes the orbitals orientation. It can have values between l and -l, including the number zero. Thus,
ml = -l, … 0… +l
From the above formula, we can write that when l = 0, ml = 0. What this means is that within the s subshell there is only one type of orbital, and this orbital is called the s orbital.
When l = 1, ml = -1, 0, +1. What this means is that within the p subshell, there are three different types of p orbitals. One with ml = -1, another with ml = 0, and the last with ml = +1.
In general, for a subshell of quantum number l, there will be 2l + 1 total orbitals within it. And orbitals within the same subshell will have the same energy.
In general, for a shell of quantum number n, the total number of orbitals in it will be equal to n2, where n is the principal quantum number. Therefore, if n = 3, the total number of orbitals in it will be 32, which is equal to 9 orbitals in total. And you can calculate total number of electrons that can fill up these orbitals by using the formula: 2n2, where n starts from 1,2,3, and so on. So, we can calculate the total number of electrons that can fill up n = 3 principal energy level as: 2(32) = 18 electrons.
The fourth quantum number is called the electron spin quantum number.
It is represented by the symbol ms, and it describes two possible spin states in which an electron can exist in an atom. To visualize these states, let’s use the following spheres to depict an electron rotating about its axis:
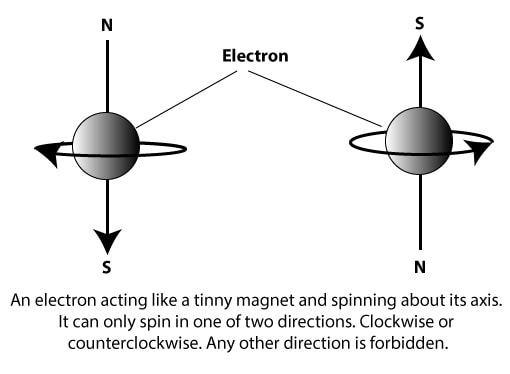
As the electron spins, it generates a magnetic field around it, and it acts as if it is a tinny bar magnet with a north and a south pole. When an external magnetic field is present, an electron can spin either clockwise or counterclockwise. When an electron spins clockwise or counterclockwise, it generates slightly different energies. This difference in energy splits the atom’s spectral lines into closely-spaced pairs.
The spin quantum number is usually assigned one of two valules. These values are +1/2 or -1/2. When two electrons have the same spin quantum number, they are usually referred as having parallel spins. That is when both have an ms of -1/2 or both have an ms of +1/2. On the other hand, when two electrons have opposite spin quantum number and occupy the same orbital, they are usually referred as paired. In this case, one electron is assigned an ms of -1/2, while the other is assigned an ms of +1/2.
As a result of the way an electron reacts to an external magnetic field, Wolfgang Pauli proposed a rule to help us fill atomic orbitals with electrons. His rule called the Pauli exclusion principle states that: you cannot fill an atomic orbital with more than two electrons. And anytime you have two electrons in an orbital, each electron must have a spin opposite the other. Another way of saying the samething is that no two electrons in the same atom can have all four quantum numbers the same. This follows that if we decide to fill the 2p orbital with two electrons, then one electron will have a spin of +1/2, while the other will have a spin of -1/2. Together, they will be paired in the 2p orbital.
To learn how to fill atomic orbitals with electrons, click here.