In chemical reactions, reactants are converted into products. In other words, atoms of reactants in the starting mixture regroup in new ways to form new chemicals called products in the product mixture. Since we can’t see atoms with our eyes, one way we can make sense of these atoms reacting is to consider them as particles interacting with one another. Because of this, when hydrogen molecules (H2) react with nitrogen molecules (N2) to form ammonia molecules (NH3), we can write a balanced chemical equation for it as:
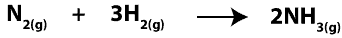
Now, imagine that before the reaction starts, we zoomed in really close and saw molecules of H2 and N2, which we drew its particle model as:
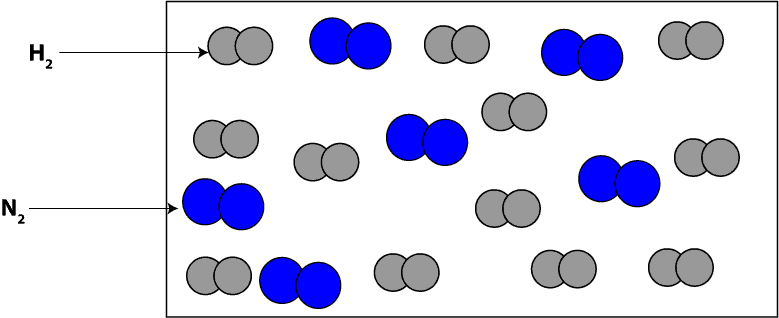
How do we interpret the particle model in terms of moles?
To interpret the particle model in terms of moles, we will count the number of each type of molecule in the model and then attach moles to the number. If we count, you will notice that we have 12 moles of hydrogen (H2) molecules and 6 moles of nitrogen (N2) molecules.
Now, which of the two chemicals is the limiting reactant and which is in excess?
To determine the limiting reactant, we will divide the moles of each reactant by its corresponding coefficient in the balanced chemical equation:
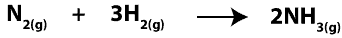
From the equation, you will notice the coefficient (number in front of chemical symbol in equation) of N2 is 1 and the coefficient of H2 is 3.
If we divide the moles of each reactant from the particle model by its corresponding coefficient from the balanced equation, we will get:
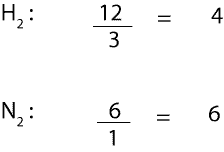
From the calculation, the smallest mole-to-coefficient ratio is the limiting reactant. Therefore, we can all agree that H2 is the limiting reactant. It is the limiting reactant because it is the chemical that is used up first in the reaction, while N2 is in excess.
If N2 is in excess, how much of it remains in the product mixture after all the limiting reactant (H2) is used up?
To figure this out, we must first determine how much of the excess reactant (N2) will react with the limiting reactant (H2). To do this, we will use the balanced chemical equation to write mole- mole ratios between N2 and H2, and then, we will pick the right ratio to use. Here are the ratios:
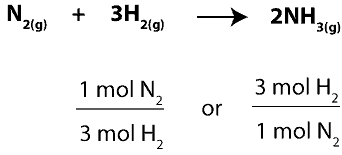
Since we want to figure out the moles of N2 that will react with H2, we will pick the ratio with N2 on top. Therefore, the complete setup for our calculation will appear as:
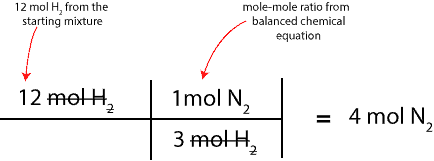
As we can see, 4 mol of N2 will react with all the 12 mol of H2 in the starting mixture to form NH3. So, the next question is, how much of the excess reactant is still in the product mixture after the reaction is complete? To determine this, we will simply subtract 4 mol of N2 from the starting moles of N2 in the starting mixture. If we do, we will get 2 moles; That is: 6 mol N2 – 4 mol N2.
The next question is, how many moles of ammonia (NH3) will be formed after all the limiting reactant is used up?
To determine this, we will convert moles of the limiting reactant (H2) to moles of NH3. To do this, we will use the balanced chemical equation to write the mole-mole ratio between H2 and NH3, and then, setup a table similar to the one above. Here is the table:
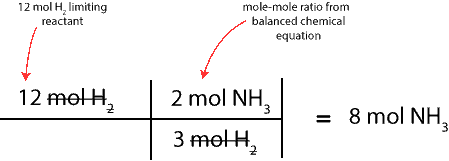
As you can see, 8 mol NH3 is expected to form after all the 12 mol H2 completely reacts with the 4 mol N2.
Now, let’s test our understanding.
Which of the following particle models depicts the product mixture after all the limiting reactant (12 mol H2) is completely used up in the reaction?
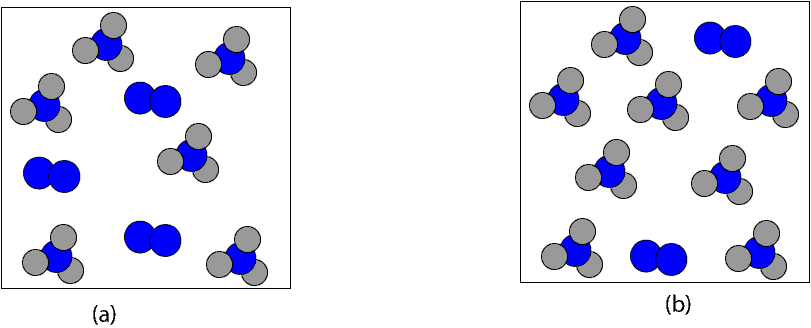
If we are both correct, then, we can clearly say that it is particle model b. If it’s particle model b, then, the next question is, how much is 8 mol NH3 in grams. To determine this, we will multiply the 8 mol NH3 by its molar mass, 17.03 g/mol. Here is a table summarizing the calculation:
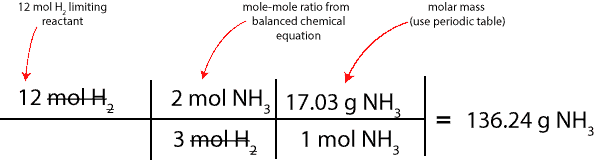
Therefore, 136.24 g NH3 is the maximum amount of NH3 we can possibly make from 12 mol H2. This maximum amount is usually called the theoretical yield.
