Both Bohr and Schrodinger assumed that in an atom there are permitted electronic states in which an electron has constant total energy. However, Bohr and Schrodinger differed in how they described the motion of an electron in these permitted electronic states.
Bohr assumed that each permitted electronic state corresponds to a specific permitted orbit. He called this permitted orbit principal quantum number, represented by n, which takes whole number values 1, 2…. and so on. As an electron travels in an orbit around the nucleus like the way planets do around the sun, its total energy would remain constant. By comparing the movement of invisible tiny electrons around the nucleus to the movement of huge visible planets around the sun, Bohr described the motion of an electron as if they were planets. Meaning he could pinpoint the exact location of an electron in an atom much like how Astronomers pinpoint the location of planets by bouncing off light of them into a microscope. Because of this, the mathematical equations he used to describe an electron’s motion could not correctly predict the properties of multielectron atoms observed in experiments. Because of this inconsistency a new theory was needed and that is where the quantum mechanical model comes in.
Just like astronomers, to see an electron, we must bounce off light of it into our microscope, but because of an electron’s small size, the strike of light causes it to change its position by the time the light returns to our microscope. Because of this, we can’t determine the position and momentum of an electron at the same time. Some uncertainty must exist in how we measure one or the other or both. Because we can’t be sure of the exact path of an electron, we can’t use the same equations astronomers use to describe the path of planets to describe path of tiny electrons inside an atom. As a result, we must use probability to describe the location of an electron in a certain region of an atom. This probability will depend on the size of the region with respect to the nucleus and other factors.
Schrodinger took all these factors into account to generate his equation called the Schrodinger equation. Solutions of the equation called wave-functions are used to generate three quantum numbers associated with each electronic state called orbital.
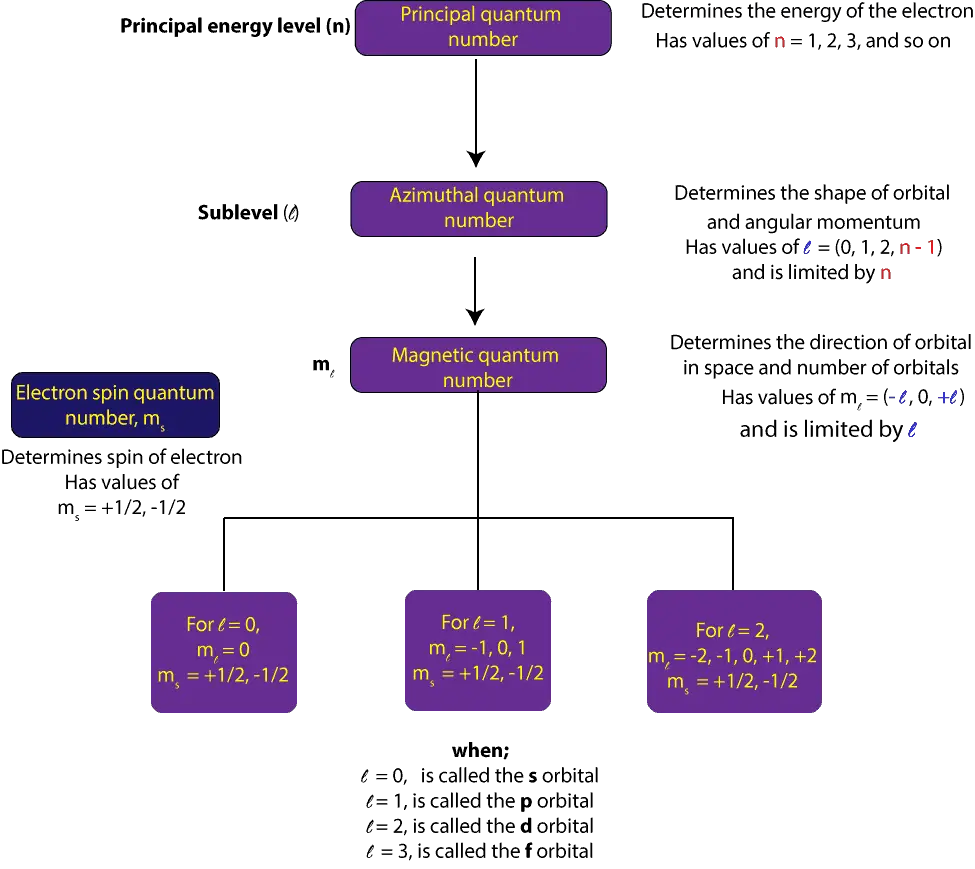
The first is called the principal quantum number, denoted by n. This quantum number determines the energy of an electron and it’s the same quantum number in Bohr’s model. It takes whole number values 1, 2, 3, 4, and so on.
The second is called angular momentum quantum number, denoted by l. This quantum number determines the shape of orbitals (sublevels). The values it takes are limited by the values of n and include l = 0, 1,2,3,4, —— (n – 1). When l = 0 it’s called the s-orbital, l = 1, the p-orbital, l = 2, the d-orbital, l = 3, the f orbital, l = 4, the g-orbital, l = 5, the h-orbital.
The third is called the magnetic quantum number, denoted by ml. This quantum number determines the number and orientation of orbitals in a sublevel. The values it takes are limited by l and can generally be represented as ml = (-l, 0, +l). When l = 1, values of ml = -1, 0, 1. These values tell us there are three p-orbitals.
Although the Schrodinger equation describes the motion of an electron, it didn’t provide a way to distribute electrons in orbitals of many electron atoms. As a result, a fourth quantum number was necessary to account for the periodic system and magnetic properties of atoms.
This fourth quantum number is called the spin quantum number, denoted by ms. This quantum number restricts the number of electrons an orbital can take, and that only two electrons can fill any orbital and these electrons must have opposite spins. This restriction is sometimes called the Pauli exclusion principle, which is stated in another way as “no two electrons in an atom can have the same identical set of four quantum numbers.” The values spin quantum number takes are limited to +1/2 or -1/2.
For instance, the four quantum numbers associated with the two electrons when n =1 are:
For first electron: n =1, l = 0, ml = 0, ms = +1/2
For second electron n= 1, l = 0, ml = 0, ms = -1/2
As you can see, since the spin quantum number are of opposite sign, we usually say that the two electrons in an orbital must have opposed spins or paired spins. If we depict an electron with an arrow, here is an illustration showing paired or opposed spins with one arrow pointing up and the other pointing down.
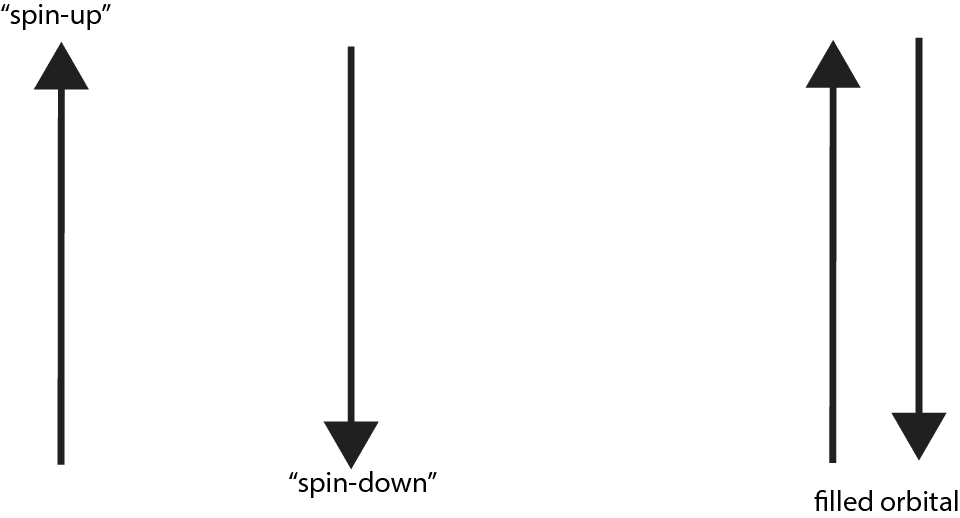
And here is a summary of the four quantum numbers:
If you want to learn more about the quantum mechanical model of an atom, click here
