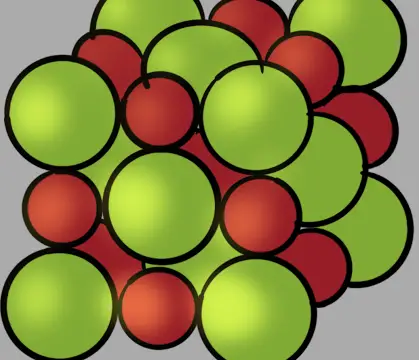
The particles in crystalline solids are arranged in an orderly repeating pattern held together by attractive forces between the particles. This orderly arrangement forms a three-dimensional structure called the crystal lattice
If the crystal is ionic, it usually consists of regular arrangement of ions. Example, sodium chloride (NaCl).
If the crystal is molecular, it usually consists of regular arrangement of molecules. Example, iodine (I2).
If the crystal is metallic, it usually consists of regular arrangement of atoms in a sea of delocalized electrons. Example, gold (Au)
If the crystal is macromolecular, it usually consists of regular arrangement of covalently bonded atoms to form a large structure. Example, diamond, graphite
What is a unit crystal?
A unit cell is the smallest piece of a crystal that when repeatedly piled without gaps between unit cells will reconstruct the entire crystal.
Here is an illustration of sodium chloride (NaCl) unit cell:
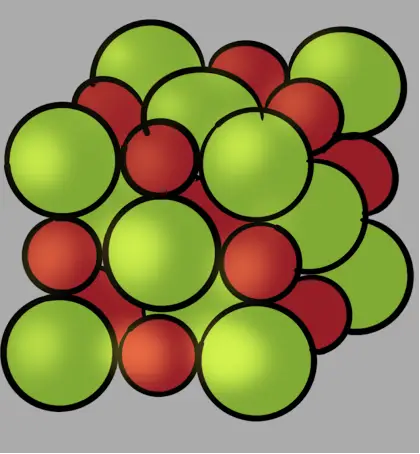
The green balls are chloride ions (Cl–) and red balls are sodium ions (Na+)
X-ray crystallography, which is used to determine the unit cell, shows chloride and sodium ions touch each other at the edges.
In a unit cell a particle at a corner, edge, and face is shared by other unit cells. This means only a fraction of these atoms is within the unit cell.
Therefore, a particle at a corner is shared by eight other unit cells. As a result, only one eighth of that particle is within the unit cell.
A particle on an edge is shared by four other neighboring unit cells. As a result, only one fourth of that particle is within the unit cell.
A particle on a face is shared by two other neighboring unit cells. As a result, only half of that particle is within the unit cell.
A particle in the body of the unit cell belongs only to that unit cell.
As you can see, we can determine the total number of particles in a unit cell by counting the number of particles in each position (corner, edge, face, and body) and multiply by the fraction of particle within the unit cell.
Now, let’s answer the following question:
The unit cell for compound Q is represented by the diagram below. Use it to answer the following questions:
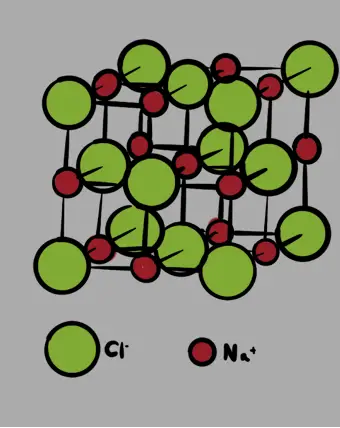
- What is the total number of sodium (Na) ions and Chlorine (Cl) ions within one unit cell?
- What is the formula for compound Q
- If the length of one face of the unit cell is 5.62 Å (Angstroms) calculate the density of compound Q in grams per cubic centimeters (g/cm3)
To determine the total number of atoms in unit cell, first, will count the number of chloride ions (Cl–) at the corners, and then multiply the number by 1/8. Second, will count number of sodium ions (Na+) on the edges, and then multiply by 1/4. Third, will count number of chloride ions on the face, and then multiply by 1/2. Fourth, will count number of sodium ions in body. Finally, will sum all the atoms from each location to get the total number of atoms for each type of ion. Here is a table summarizing the calculation

So, for question (a) the total number of sodium ions (Na+) is 4 and total number of chloride ions (Cl–) is 4.
For question (b), the formula for compound Q is NaCl. How did we go from Na4Cl4 to NaCl? Since 4 divided by 4 is 1. We can further simply the subscripts in Na4Cl4 to NaCl. Another way of saying this is that since there are 4 positive sodium ions and 4 negative chloride ions, the charges cancel out to give NaCl an overall charge of zero.
For question (c), to calculate the density of the unit cell, and since Density is mass divided by volume (D = m/v), we must convert the number of sodium and chloride ions to mass in grams and determine volume of unit cell from length of unit cell.
To do, will apply the mole concept to convert 4 atoms of Na and 4 atoms of Cl to moles of Na and from moles to mass of Na and Cl. Once we get grams for both ions, will add them to get grams of unit cell. Here is how to calculate it:

From the calculation, the mass of NaCl is 3.89 x 10-22 g
For volume, we must recognize that the question demands we report density in units of grams per cubic centimeters. If so, must recall that 1 Å = 1 x 10-10 m and 1 m = 100 cm. Once we do, will convert length of unit cell in Angstroms to cm. Once we get length in centimeters, and since a unit cell is a cube with equal sides, we will multiply the length by itself three times (length x width x height) to get the volume of unit cell in cubic centimeters (cm3). Here is the calculation:

Therefore, volume of unit cell = 5.62 x 10-8 cm x 5.62 x 10-8 cm x 5.62 x 10-8 cm = 1.78 x 10-22 cm3
To calculate density, will divide mass of unit cell by volume of unit cell, here is the calculation:
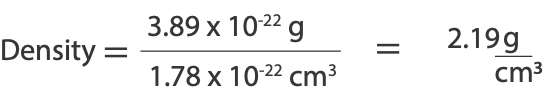
Hence density of NaCl unit cell is 2.19 g/cm3
To learn how NaCl dissolves in water, click here.